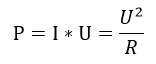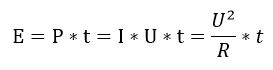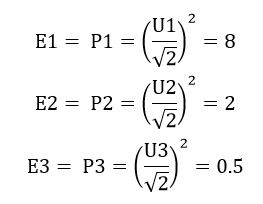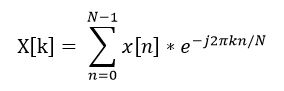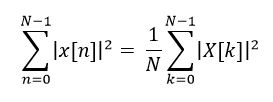在对脑电信号做分析的时候，经常看到频谱、能量、功率谱和功率谱密度这些词，在一些论文中用的也比较随意，确实好像不论说其中哪一个我们总能理解指向一个东西，仿佛这些词的表示是一致的。真的是让人很难受，所以写这一篇来扒开看看，它们之间的关系。

软件环境

MATLAB 2016a

正文

首先构建一个简单清晰的信号来引出下概念

Fs = 1000;
T = 1/Fs;
time = 1;
L = Fs* time;
t = (0: L-1)* T;
x1 = 4* sin(2* pi* 10* t);
x2 = 2* sin(2* pi* 20* t);
x3 = 1* sin(2* pi* 30* t);
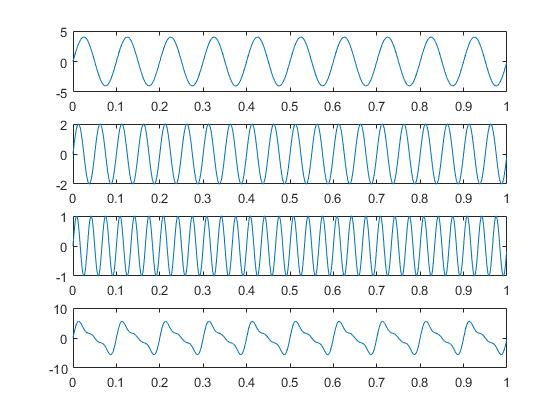
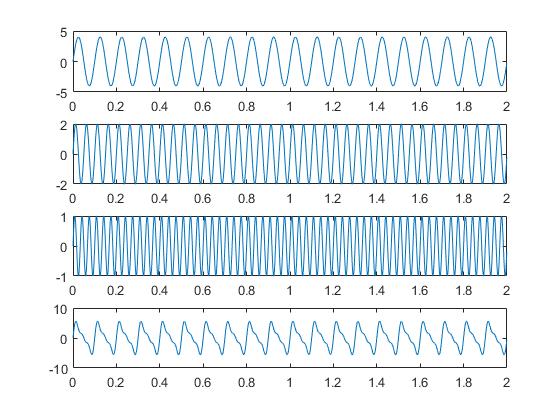
x =  x1+ x2+ x3;

上面代码构建了一个由3个正弦信号构成的模拟信号x，这三个正弦信号频率分别为10Hz、20Hz和30Hz，幅值分别为4、2和1，采样频率为100Hz。我们将这个信号当做一个简单脑电信号，这时候幅值被赋予了电压意义，为了方便表述，不考虑量纲，截取1秒时间(1000个采样点)，如图1所示

初中物理告诉我们，电信号做功功率公式为

还有能量公式为

现在时间t前面说了取了1秒，设电阻R等于1欧姆。这时候发现E = P = U²，是的因为这是单位时间1秒，能量和功率在数值上是相等的。

初中物理还指出了，相同时间内，正弦信号的交流电所做的功，等于其电压有效值这么大的直流电所做的功，而正弦信号电压有效值等于其峰值除以 ，于是x1、x2和x3这三个正弦分量的能量和功率为

对于合成信号x的能量在数值上是E1、E2和E3的和。

到这里开始频域的讨论了，于是对合成信号x做傅里叶变换

fx = fft(x);
ft = Fs* (0: L/2-1)/L;
fxP2 = (fx./ L).* (conj(fx)./ L);
fxP1 = fxP2(1: L/2);
fxP1(2:end) = 2* fxP1(2:end);

使用快速傅里叶变换算法fft计算合成信号x的离散傅里叶变换，根据傅里叶变换公式知道得到的fx是复数，但是复数我们还没法画出图形了，需要将其值的模求出来。下面放出离散傅里叶变换公式

这时候的模叫做双边谱fxP2，双边谱是中间对称的，两边一模一样，因为根据奈奎斯特采样定理频率范围只有采样频率的一半，于是还需要进行折中得到单边谱，单边谱的值是双边谱的和即两倍，除了第一个点，这是由傅里叶变换的性质决定的，从傅里叶变换公式中e^-j2πkn/N欧拉展开可以知道，这里不讲这个。

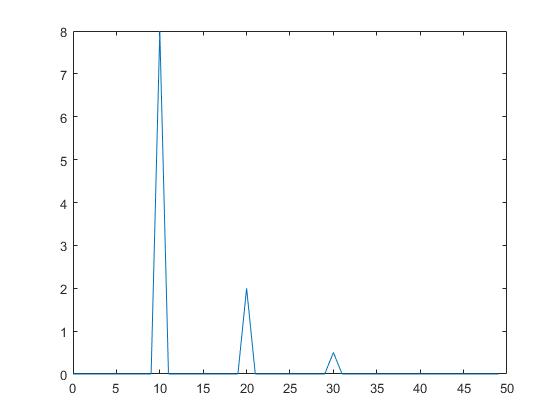
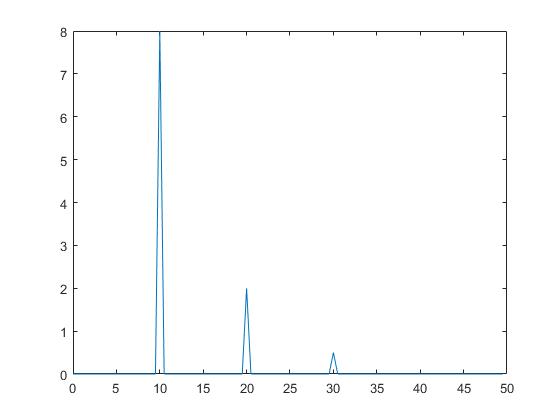
如图2所示是合成信号x傅里叶变换单边幅度谱。

好了现在说说图2的内容，横坐标是频率单位是Hz，正好对应了10、20和30三个频率点，为什么是尖峰不是脉冲是因为这个画图是连起来的，前后点都是0，只是连起来了而已，这个好理解，那纵坐标是什么呢。我们看到三个频率点对应的值分别是8、2和0.5，似曾相识，它们是跟前面求出来的E和P是一样的，那这个单边幅度谱的纵坐标到底是能量还是功率呢。

我们先从理论上来推测一下到底是什么，说到时域频域还有能量功率什么的，很难让人不想起帕塞瓦尔定理，帕塞瓦尔定理指出一个信号所含有的能量恒等于此信号在完备正交函数集中各分量能量之和，对应了傅里叶变换的一个性质，它表明了信号的能量在时域和频域是相等的。下面是离散的帕塞瓦尔能量守恒等式

公式前面是信号在时域的能量，前面通过有效值求出来了，分别是8、2和0.5。但是这里离散信号其实是无量纲的，也即这1秒对应的1000个采样点，在无量纲的情况下其实应该是认为1000秒，能量也就是8000、2000和500。

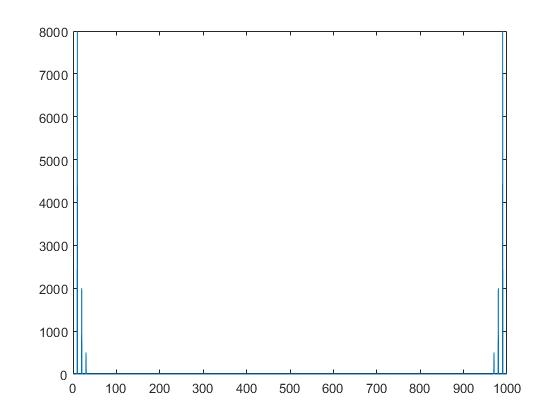
下面我们按照帕萨瓦尔公式画出对应的频域值

ftE = Fs* (0: L-1)/L;
fE = fx.*conj(fx)/L;

显然根据帕塞瓦尔公式求出的值确实是与时域能量相等的，那么我们可以确定图三的纵坐标就是能量值了，而这个能量谱图是由“fx.*conj(fx)/L”计算出来的，跟前面画单边谱的公式比较一下“(fx./ L).* (conj(fx)./ L)”，发现单边谱计算公式多除以了一个L，也即采样点数量，在离散无量纲的情况下就是时间，能量除以时间就是功率，所以至此推出单边谱的纵坐标是功率。

根据帕塞瓦尔定理我们推测出了这个单边幅度谱的纵坐标是功率，不同频率对应的功率，下面再用实验验证一下是不是这样的。

前面是因为时间取了单位时间1秒导致了能量和功率在数值上相等，那把时间不取单位时间不就好了吗，下面是2秒的时域数据，如图3所示

同样的来画出2秒(2000个采样点)时间的单边幅度谱看看

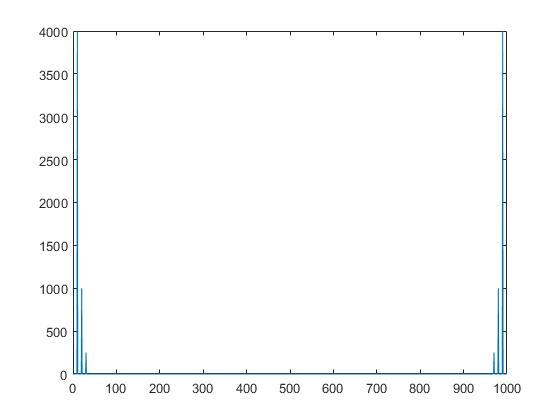
可以看出图5与图2几乎没有区别，只有横坐标更加密集了，这是因为采样点增大了1倍导致的，纵坐标值依然是8、2和0.5，这也证明单边幅度谱确实是功率，如果是能量，信号时间增长了一倍，能量也应该增长一倍才对，下面就画出2秒合成信号x的频域能量图

对比图6和图3发现能量确实增长了1倍。

总结一下，时域信号的能量求法，离散信号的能量就是幅值平方的累加和，连续信号则是平方的积分。

对时域信号做傅里叶变换后对其值求模，得到的谱叫做频谱的幅度谱，它的纵坐标没有物理量纲，这个幅度谱与相位谱在一起称为频谱。

在对傅里叶变换后的值做进一步处理，具体叫什么谱视纵坐标而定，如果纵坐标是能量，就叫能量频谱即频域能量谱，这里区分时域的能量，时域能量是时间对应的能量，能量频谱则是频率对应的能量；如果是功率，就叫功率频谱即频域功率谱。而能量频谱与功率频谱之间是一个线性关系，他们差了一个信号时长的倍数。

再说功率谱密度，它和功率谱本质上是一个东西，功率谱指的是整个一个谱，是一个频率序列，功率谱密度这是指某个具体频率值对应的功率值。人们习惯上将二者不加区分，经常混用，都是指代频率点处的功率值。

在脑电信号的处理中，常常使用Welch法来估计信号的功率谱密度，Welch法基于周期图功率谱密度估计法，通过对信号进行加窗将原始信号拆分成多个数据段，而数据段之间可以重叠，在MATLAB函数pwelch中提供了两个参数用以调整窗口和重叠的大小。下面使用Welch法来求一下2秒长度合成信号x的功率谱密度。

nfft = 2^nextpow2(L);
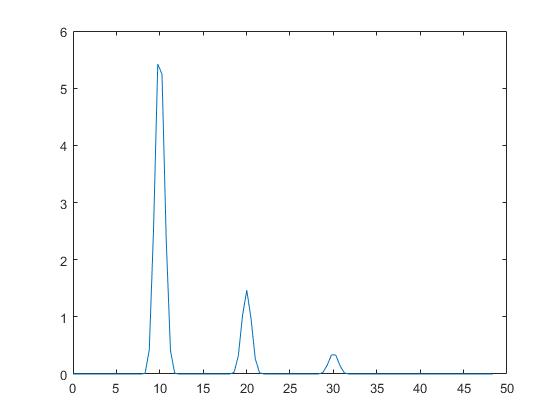
[fxPw, ftW] = pwelch(x, 1000, 500, nfft, Fs);

取加窗长度为1000个采样点即1秒，重叠0.5秒，这样就是截取了3段数据。Welch法估计功率谱密度曲线如图7所示。

从图中可以看出Welch法估计的功率谱密度是存在一定方差的，但是信号的峰值主要部分还是可以比较精确的表示出来。

点击下载全部代码和数据

或扫码搜索关注微信公众号“燕山徐一”，后台回复“脑电频谱”获取代码。

赏