对应上一篇使用DATA1和DATA2的CSP特征进行SVM运动想象分类，这一篇写卷积神经网络CNN对这两个数据集的功率谱特征进行运动想象分类demo。有关数据集的介绍阅读上一篇文章即可，这里不再重复。

软件环境及数据背景

MATLAB2016a + Python 3.7 + PaddlePaddle 2.0.1，matlab处理数据格式为mat，python处理数据格式为npy。

正文

关于脑电功率谱特征提取在之前的预处理一文中已经写过，这里也只是对函数稍作改动，直接拿来用了。关于CNN使用的是百度的paddle深度学习框架，为什么选这个，主要还是因为支(wo)持(hen)国(pin)产(qiong)，用paddle可以薅百度GPU羊毛，不然自己电脑跑可能慢不说，分分钟死机。就体验来说对新手不算友好，尤其是1.x版本，之前也写了一个1.x版本的，后来过年那段时间推出2.x版本，逐步废弃1版本的一些API，同时也增加了很多高层API，感觉是要简单很多了。

首先还是准备数据，合并数据带通滤波，与SVM-CSP是一样的操作，功率谱特征提取函数如下：

function [ pxx,fpow,avgPsdFeatures ] = psdSort( inSignal,fs )
% ---------------------------------
%    求功率谱密度以及各个节律频带的信号功率
% ---------------------------------
% INPUT:
%   inSignal  输入信号
%   fs  采样频率
% OUTPUT:
%   pxx  功率谱密度
%   fpow  频率向量
%   psdFeatures  各节律频带的平均功率组成的数组

    [pxx, fpow] = pwelch(inSignal, [], [], [], fs);
    psd_alpha = bandpower(pxx, fpow, [8, 14], 'psd');
    psd_beta = bandpower(pxx, fpow, [14, 30], 'psd');
    avgPsdFeatures=[psd_alpha,psd_beta];
    
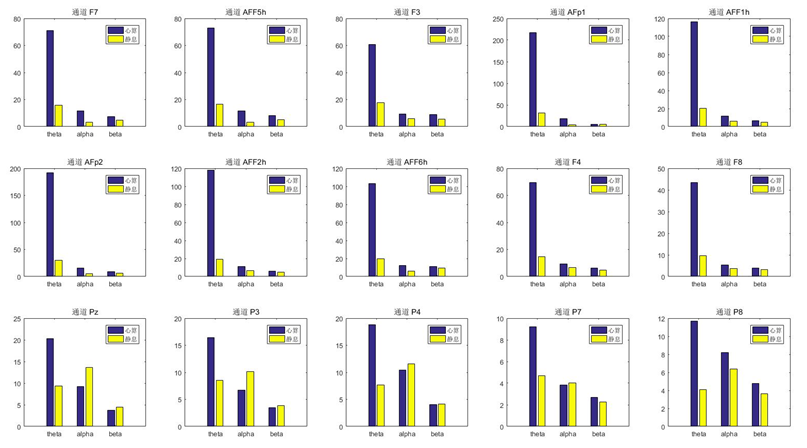
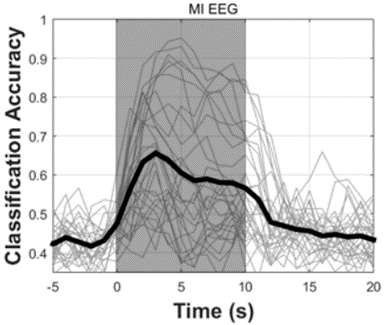
end

其中提取出alpha和beta两个节律的平均功率是最开始为了能不能从大范围上观察出有什么特别的趋势，使用的是DATA1数据集均匀抽取一下样本观察，不过看的是心算范式，如图1所示。

得到DATA1数据集PSD特征共1740个样本，DATA2数据集PSD特征共6520个样本，区别在于DATA1采样点2000，因为10秒数据采样频率200Hz，DATA2采样点1000，因为4秒数据采样频率250Hz，故PSD特征数据长度也是2:1关系，根据各自通道确定其输入数据shape分别为[None, 1, 3, 129]和[None, 1, 9, 257]。同时也因为二者通道数的差别，网络部分参数也做了一些适应，以DATA2训练网络为例，代码如下：

class DATA2Net(paddle.nn.Layer):
    def __init__(self, num_classes=2):
        super(DATA2Net, self).__init__()

        self.conv1 = paddle.nn.Conv2D(in_channels=1, out_channels=32, kernel_size=(1, 3))
        self.pool1 = paddle.nn.MaxPool2D(kernel_size=(1, 4), stride=(1, 4))

        self.conv2 = paddle.nn.Conv2D(in_channels=32, out_channels=64, kernel_size=(2,3))
        self.pool2 = paddle.nn.MaxPool2D(kernel_size=(1, 4), stride=(1, 4))

        self.conv3 = paddle.nn.Conv2D(in_channels=64, out_channels=64, kernel_size=(1,3))

        self.flatten = paddle.nn.Flatten()

        self.linear1 = paddle.nn.Linear(in_features=640, out_features=128)
        self.dropout = paddle.nn.Dropout(0.3)
        self.linear2 = paddle.nn.Linear(in_features=128, out_features=num_classes)
    
    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.pool1(x)

        x = self.conv2(x)
        x = F.relu(x)
        x = self.pool2(x)

        x = self.conv3(x)
        x = F.relu(x)

        x = self.flatten(x)
        x = self.linear1(x)
        x = F.relu(x)
        x = self.dropout(x)

        x = self.linear2(x)
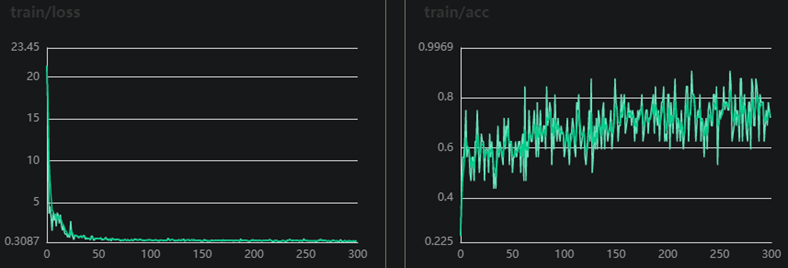
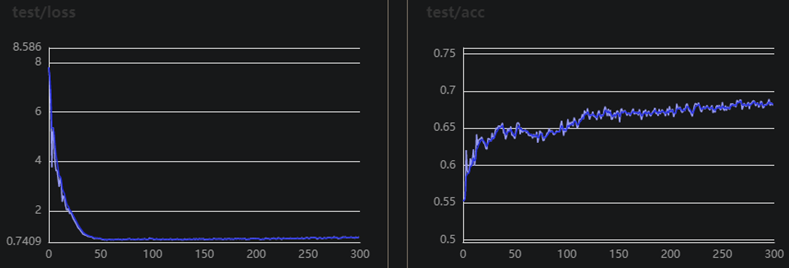
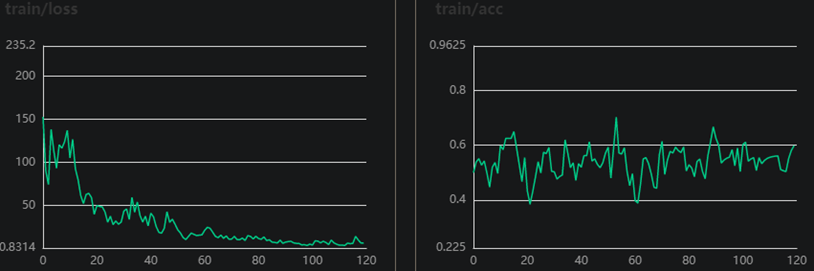
        return x

这个网络就是一个普通CNN网络，堆叠几层卷积和池化，中间用relu函数激活，由于样本不多，网络也没有很浅，训练集后面就很快过拟合了，加了个dropout层。其他参数BATCH_SIZE=32，learning_rate=0.00001，Adam优化器，训练300个epoch，训练过程如下：

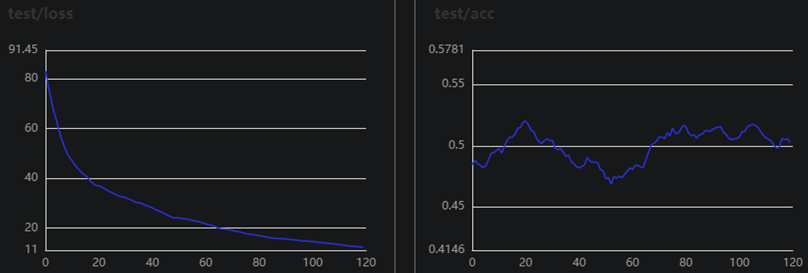
可以看出准确率达到68%之后就区域稳定了，通过调整一些参数比如增大学习率也可以达到70%，但会有些波动。这里没有用DATA1演示，因为DATA1表现非常差，网络结构没有改变，其他参数BATCH_SIZE=32，learning_rate=0.00001，Adam优化器，训练120个epoch，适应9通道改变了几个参数，如下：

class DATA1Net(paddle.nn.Layer):
    def __init__(self, num_classes=2):
        super(DATA1Net, self).__init__()

        self.conv1 = paddle.nn.Conv2D(in_channels=1, out_channels=32, kernel_size=(3, 3))
        self.pool1 = paddle.nn.MaxPool2D(kernel_size=(2, 4), stride=4)

        self.conv2 = paddle.nn.Conv2D(in_channels=32, out_channels=64, kernel_size=(2,3))
        self.pool2 = paddle.nn.MaxPool2D(kernel_size=(2, 4), stride=4)

        self.conv3 = paddle.nn.Conv2D(in_channels=64, out_channels=64, kernel_size=(1,3))

        self.flatten = paddle.nn.Flatten()

        self.linear1 = paddle.nn.Linear(in_features=832, out_features=128)
        self.dropout = paddle.nn.Dropout(0.3)
        self.linear2 = paddle.nn.Linear(in_features=128, out_features=num_classes)
    
    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.pool1(x)

        x = self.conv2(x)
        x = F.relu(x)
        x = self.pool2(x)

        x = self.conv3(x)
        x = F.relu(x)

        x = self.flatten(x)
        x = self.linear1(x)
        x = F.relu(x)
        x = self.dropout(x)
        x = self.linear2(x)
        return x

可以说是几乎不在训练了，同样的脑电特征数据，DATA2表现正常，DATA1表现拉跨，清洗方法也是同样的，我觉得是数据本身不太好。也给数据做过归一化处理，虽然我认为没必要，数据几个通道属性是一样，脑电幅值也没有多大差别，做了归一化后训练时波动确实有所改善，但是验证集准确率并没有得到改善。

在以上两个训练中，训练集和测试集之比都是4:1。

为了进一步验证，特地找来minist数据集做了测试，训练集50000个样本，验证集10000个样本，训练20个epoch，不出所料上来就达到了98.5%，很快啊。训练过程如下：

在公布这个数据集的论文中，作者使用3秒滑动时间窗提取CSP特征并使用LDA分类器分类，文中描述纯EEG信号做MI训练平均准确率为65.6%，没有查到更多DATA1数据来做研究的论文了。

文末提供了资源下载连接。关于代码使用DATA2进行演示；关于数据DATA1提供了被试01的原始数据以供参考，DATA2提供了被试01的第一组数据以供参考；关于工具箱文中使用到的bbci和biosig工具箱也已包含。

总的来说，CSP和功率谱特征都是要比DATA2数据集差，尤其功率谱在DATA1这里几乎算不上特征，但是论文作者提供的65%以及我测试的SVM-CSP也达到了65%，所以是什么原因呢，还要继续使用DATA1数据集吗？

另关于其CSP特征使用支持向量机分类demo，可阅读姊妹篇”运动想象脑电CSP-SVM支持向量机二分类”。

点击下载完整代码和数据

或扫码搜索关注微信公众号“燕山徐一”，后台回复“运动想象PSD”获取代码

赏