本文基于一个公开数据集和一个BCI竞赛数据集，提供一个SVM-CSP运动想象二分类demo。公开数据集来自论文” Open Access Dataset for EEG+NIRS Single-Trail Classification”，BCI竞赛数据集来自2008年BCI Competition中Data sets 2b数据集。

软件环境及数据背景

MATLAB2016a + pycharm-community-2020.2，Python 3.8.3 + scikit-learn 0.23.1，matlab处理数据格式为mat，python处理数据格式为npy。

公开数据集

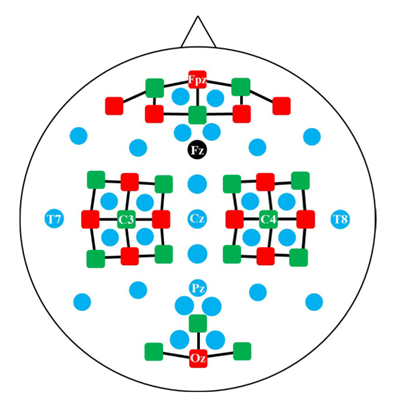
论文” Open Access Dataset for EEG+NIRS Single-Trail Classification”提供了一个使用脑电图(EEG)和近红外光谱(NIRS)的混合脑机接口(BCIs)开放存取数据集，本文只使用其中的脑电数据。有29名健康参与者(14名男性和15名女性，年龄为28.5±3.7岁)参与了数据采集，脑电采样频率为1000Hz，作者提供的数据集已经降采样到200Hz。图1位电极位置。

本文选用’FCC5h’、’FCC6h’、’FCC3h’、’FCC4h’、’Cz’、’CCP5h’、’CCP6h’、’CCP3h’、’CCP4h’ 9个通道，即图1中C3和C4周围8个通道加Cz通道。

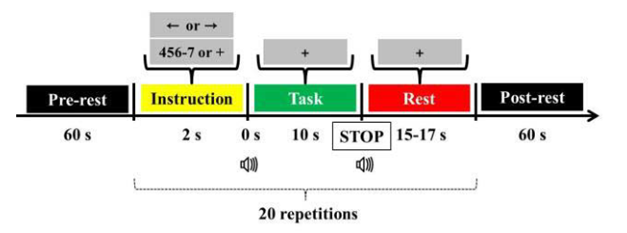
图二为左右运动想象的实验范式。

每一阶段包括1分钟的实验前休息期、20次重复给定任务和1分钟的实验后休息期。任务开始时用2秒的时间对任务进行视觉介绍，然后用10秒的时间进行任务和休息时间(从15到17秒随机分配)。详细介绍请查阅该论文。

BCI竞赛数据集

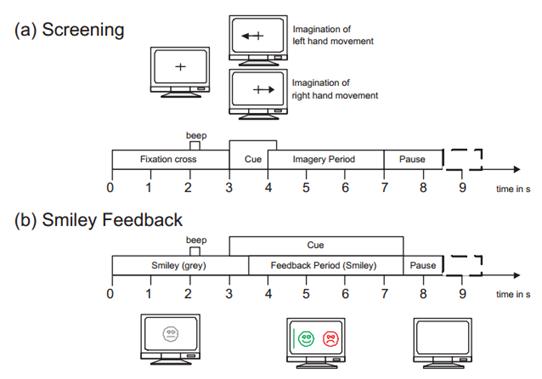
08年竞赛数据在论文中引用很多了，都比较熟悉，图3为这批数据的范式。

其中(a)对应的是01T和02T系列无反馈数据，(b)对应的是03T、04E和05E系列有反馈数据。提供数据被试有9人，每人有以上五组数据，共45组数据。记录电极为C3、C4和Cz三个通道，采样频率为250Hz，数据集下载链接为http://www.bbci.de/competition/iv/，这批数据本文将全部使用。

正文

为了方便叙述，下文将论文公开数据集记为DATA1，BCI竞赛数据集记为DATA2。根据以往论文，在数据使用之前，对数据进行了8~30Hz带通滤波，保留运动想象诱发的EＲD /EＲS现象主要集中区，mu节律(8～13 Hz) 和beta节律(14～30 Hz)，滤波器使用matlab提供的切比雪夫Ⅱ型滤波器，在通带内单调下降，阻带内等波纹，过度带宽较小。代码如下：

Wp = [8 30]/200*2;
Ws = [6 33]/200*2;
Rp = 3;
Rs = 30;
[n, Ws] = cheb2ord(Wp, Ws, Rp, Rs);
[b,a] = cheby2(n,Rs,Ws);
epo.imag = proc_filtfilt(epo.imag, b, a);

epo是DATA1合成脑电连续数据后的结构体，epo.imag是脑电运动想象数据结构体，proc_filtfilt函数由BBCI工具箱提供。使用前需要下载工具箱并添加MATLAB路径。

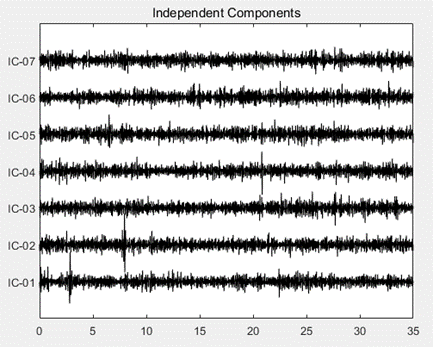
对DATA1和DATA2两批数据均只做了滤波处理后进行使用了，也尝试使用了去基线、重定义参考和去眼电等预处理操作，但分类结果表明不如只做滤波处理的效果好，尤其自动去眼电操作，因为eeglab去眼电需要凭借经验且千样本处理耗时。作者使用fastica算法将epo.imag.x数据进行独立成分提取并与DATA1中提供的两个通道眼电数据做相关度比较，去除相关度最高的两个成分。

为了不过分影响数据量，设定独立成分小于7个时，不进行去除操作，但结果仍是差了8个百分点，故只保留滤波操作。DATA2预处理与DATA1相同。

滤波后直接对数据进行CSP特征提取操作，不清楚的地方可以对照” CSP-Designing optimal spatial filters for single-trial EEG classification in a movement task”论文来看，比如程序中说的”协方差矩阵”在文中的定义，其维度即脑电通道数，还有数据格式和处理顺序导致的微小变化等。CSP特征提取函数如下：

function [ F, csp_feature, csp_label ] = CspFeature( inputData, inputLabel, featDim )
% -----------------------------------
% 求取输入数据的CSP特征
% -----------------------------------
% Output:
% F -- 空间滤波器
% csp_feature -- inputData提取的CSP特征，(采样点数,样本数)
% csp_label -- csp_feature对应的标签
% Input:
% inputData -- 输入数据，(采样点数,通道数,样本数)
% inputLabel -- inputData对应的标签，0/left，1/right
% featDim -- 提取特征对数

    channels = size(inputData, 2);
    trials = size(inputData, 3);
    CovData = zeros(channels, channels, trials);
    for i = 1:trials
        sigData = inputData(:,:,i);
        sigDataX = sigData'*sigData;
        CovData(:,:,i) = sigDataX/trace(sigDataX);
    end
    C_left = sum(CovData(:, :, inputLabel == 0), 3);
    C_right = sum(CovData(:, :, inputLabel == 1), 3);
    C = C_left + C_right;
    
    [Vc, Dc] = eig(C);
    P = diag(diag(Dc).^(-1/2))*Vc';
    S_left = P*C_left*P';
    [Vs, Ds] = eig(S_left);
    [~, index] = sort(diag(Ds), 'descend');
    Vs = Vs(:, index);
    F = P'*Vs;
    F = F(:, [1:featDim channels-featDim+1:channels]);
    
    data_left = inputData(:, :, inputLabel == 0);
    data_right = inputData(:, :, inputLabel == 1);
    left_num = size(data_left ,3);
    right_num = size(data_right ,3);
    csp_left = zeros(featDim*2, left_num);
    csp_right = zeros(featDim*2, right_num);
    for i=1:left_num
        csp_left(:, i) = log(var(data_left(:, :, i)*F));
    end
    for i=1:right_num
        csp_right(:, i) = log(var(data_right(:, :, i)*F));
    end
    csp_feature = [csp_left, csp_right];
    csp_label = [zeros(1, left_num), ones(1, right_num)];

end

输入输出参数都已经写好了注释并标注了数据格式，使用前需要确认输入数据没有NAN和全为0的样本，比如DATA2就需要对NAN进行处理。

写好CSP特征提取函数之后，合并DATA1中29个被试运动想象脑电数据，根据范式截取运动想象全部10秒的数据，为了对比DATA2将featDim设定为3，该值不能超过通道数。

得到29个被试一共1740个CSP样本，训练集与测试集之比为3:1，使用机器学习库scikit-learn提供的支持向量机算法，主要代码如下：

ss = StandardScaler()
x_train = ss.fit_transform(x_train)
x_test = ss.fit_transform(x_test)
linSvc = LinearSVC()
linSvc.fit(x_train, y_train)
y_predict = linSvc.predict(x_test)
print('The Accuracy of Linear SVC is', linSvc.score(x_test, y_test))
print('precision&recall&f1-score of Linear SVC:', '\n',
      classification_report(y_test, y_predict,
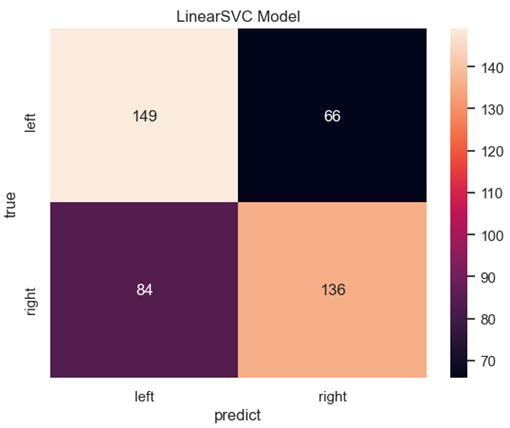
                            target_names=['左', '右']))

运行得到SVM-CSP-DATA1分类准确率为65.51%，对应的混淆矩阵如图5所示。

输出：

对于DATA2数据，9个被试，每个被试5组数据。但下载得到的是gdf格式，根据提供的数据说明文档” BCI Competition 2008 – Graz data set B”可知，可以下载biosig工具箱，将gdf格式转换为matlab处理的mat格式，需要注意的是不能使用matlab设置路径来添加biosig，这样会报错添加失败，其实在biosig>INSTALL文件中已经写了操作方法，在biosig文件夹下运行install.m文件，不要清空工作区，紧接着就可以运行加载语句了：

[BCI2bData, HDR]=sload(gdfName_list{id});

程序中BCI2bData是脑电数据，HDR是相关信息结构体，如HDR.TRIG记录着样本数，HDR.EVENT中记录着打标点等参数，作者这里直接使用样本数结合采样率来划分样本的，根据范式提取了3~7秒数据，没有使用打标点。

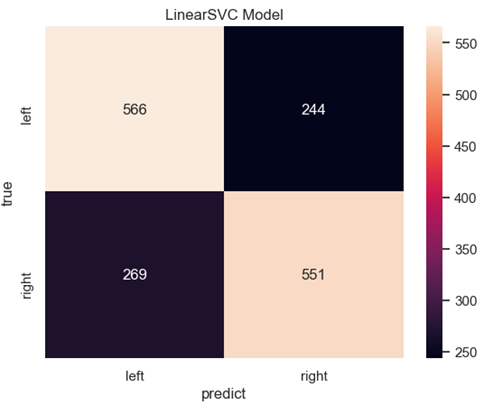
合并所有mat数据后提取CSP特征得到6520个样本，同样的训练集与测试集之比为3:1，运行分类程序得到SVM-CSP-DATA2分类准确率为68.52%，对应的混淆矩阵如图6所示。

输出：

综上SVM对两个数据集CSP特征的分类准确率分别为0.65和0.68，文末提供了资源下载连接。关于代码使用DATA1进行演示；关于数据DATA1提供了被试01的原始数据以供参考，DATA2提供了被试01的第一组数据以供参考；关于工具箱文中使用到的bbci和biosig工具箱也已包含。

另关于其功率谱特征使用CNN卷积神经网络分类demo，可阅读姊妹篇”运动想象脑电PSD-CNN卷积神经网络二分类”。

点击下载全部代码及数据

或扫码搜索关注微信公众号“燕山徐一”，后台回复“运动想象CSP”获取代码。

赏