读《python机器学习及实践-从零开始通往kaggle竞赛之路》
这几天在读《python机器学习及实践-从零开始通往kaggle竞赛之路》一书,整理了一点个人理解笔记,附上代码(对书中代码有少许改动)。
软件环境及数据背景
pycharm-community-2020.2 + Anaconda3-2020.07-Windows-x86_64 + Python 3.8.3 + PyTorch,网上有很多系列安装教程,建议不明白的,安装之前把之前安装的所有python解释器等全部删除干净,一步步重新装。
第一章是一点python编程基础,从第二章开始。
监督学习经典模型
在机器学习中,根据目标预测变量的类型不同,分为两类,预测值为连续时称作“回归预测”,预测值为离散时称作“分类学习”。
分类学习
分类学习是最常见的监督学习问题,有二分类、多分类和多标签分类等。
线性分类器
线性分类器(Linear Classifiers)是一种假设特征与分类结果存在线性关系的模型,模型通过对数据的多个特征维度进行各自的算法计算来做决策。
这一节介绍了对数几率回归和模型和随机梯度下降模型,使用这两种模型对一套“良性/恶性乳腺癌肿瘤预测”数据分别做了实践。首先我已将breast-cancer-wisconsin.data数据下载到本地,该套数据包含699组样本,其中有16例有参数缺失,每组样本11列,第一列是用于检索的id number,第11列是肿瘤类型分类,只有两种取值,2为良性,4为恶性,中间九组是肿瘤的医学特征,也即用来学习的特征,每种特征数值已被量化为1~10数字,具体是什么含义不做了解。处理代码如下:
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
'''良性/恶性乳腺癌肿瘤数据预处理'''
# 创建特征列表
column_names = ['Sample code number', 1, 2, 3, 4, 5, 6, 7, 8, 9, 'class']
# 读取原始乳腺癌肿瘤数据
data = pd.read_csv('breast-cancer-wisconsin.data', names=column_names)
# 将?替换为标准缺失值np.nan表示
data=data.replace(to_replace='?', value=np.nan)
# 删除所有含缺失值的行
data = data.dropna(how='any')
print(data.shape)
# 无缺失值数据683条,每条样本包含检索ID一个+9个医学特征+一个肿瘤分类
print(data.head())
'''分割良性/恶性乳腺癌肿瘤训练、测试数据 3:1'''
x_train, x_test, y_train, y_test = train_test_split(
data[column_names[1:10]],
data[column_names[10]],
test_size=0.25,
random_state=11)
print('训练样本良性2/恶性4分布:', '\n', y_train.value_counts(), '\n',
'测试样本良性2/恶性4分布:', '\n', y_test.value_counts()), '\n'
'''使用线性分类模型(Logistic回归与随机梯度参数估计)预测良性/恶性肿瘤'''
# 标准化数据,保证每个维度的特征数据方差为1,均值为0,使得预测结果不会被某些维度过大的特征值主导
ss = StandardScaler()
x_train = ss.fit_transform(x_train)
x_test = ss.fit_transform(x_test)
# 初始化LogisticRegression、SGDClassifier
lr = LogisticRegression()
SgdC = SGDClassifier()
# 调用LogisticRegression中的fit函数/模块用来训练模型参数
lr.fit(x_train, y_train)
# 使用训练好的模型lr对测试集进行预测
lr_y_predict = lr.predict(x_test)
# 调用SGDClassifier中的fit函数/模块用来训练模型参数
SgdC.fit(x_train, y_train)
# 使用训练好的模型lr对测试集进行预测
SgdC_y_predict = SgdC.predict(x_test)
'''使用线性分类器模型分析之前的预测性能'''
# 分别使用Logistic模型和随机梯度下降模型自带的评分函数score获得模型在测试集上的准确性结果
print('Accuracy of LR Classifier:', '\n', lr.score(x_test, y_test), '\n',
'Accuracy of SGD Classifier:', '\n', SgdC.score(x_test, y_test)), '\n'
# 分别使用Logistic模型和随机梯度下降模型获得青雀,精确率&召回率&F1指标三个指标结果
print('precision&recall&f1-score of LR Classifier:', '\n',
classification_report(y_test, lr_y_predict, target_names=['良性', '恶性']), '\n',
'precision&recall&f1-score of SGD Classifier:', '\n',
classification_report(y_test, SgdC_y_predict, target_names=['良性', '恶性']), '\n',
)
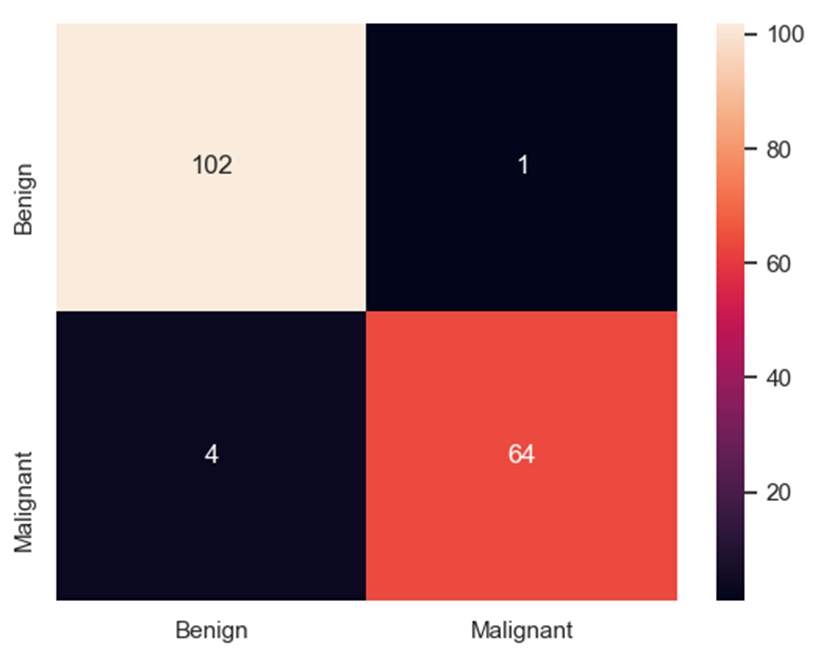
# 求取两种模型预测结果的混淆矩阵
cmLrDf = pd.DataFrame(confusion_matrix(y_test, lr_y_predict),
index=['良性', '恶性'],
columns=['良性', '恶性'])
cmSgdCDf = pd.DataFrame(confusion_matrix(y_test, SgdC_y_predict),
cmLrDf.index, cmLrDf.columns)
print('LR混淆矩阵:', '\n', cmLrDf, '\n',
'SgdC混淆矩阵:', '\n', cmSgdCDf)
# 设置Seaborn绘图风格默认
sns.set()
sns.heatmap(cmLrDf, annot=True, fmt="d",
xticklabels=['Benign', 'Malignant'],
yticklabels=['Benign', 'Malignant'])
plt.show()除了混淆矩阵这块是我自己添加的,其他大部分与书中代码一致,注释也很详细。有一点关于transform的,transform使用前需要先fit,标准化(0,1)分布,fit_transform与transform的区别网上有很多讲的,我简单说下我的理解:书中对于测试集没有fit,是因为训练集fit过了,测试集使用的训练集的参数。下面分析运行结果。
| 显示前五行数据以供直观观察: (683, 11) Sample code number 1 2 3 4 5 6 7 8 9 class 0 1000025 5 1 1 1 2 1 3 1 1 2 1 1002945 5 4 4 5 7 10 3 2 1 2 2 1015425 3 1 1 1 2 2 3 1 1 2 3 1016277 6 8 8 1 3 4 3 7 1 2 4 1017023 4 1 1 3 2 1 3 1 1 2 分割训练和测试样本: 训练样本良性2/恶性4分布: 2 341 4 171 测试样本良性2/恶性4分布: 2 103 4 68 Logistic回归与随机梯度参数估计两种模型的准确性: Accuracy of LR Classifier: 0.9707602339181286 Accuracy of SGD Classifier: 0.9766081871345029 Logistic回归与随机梯度参数估计两种模型精确率&召回率&F1指标参数: precision&recall&f1-score of LR Classifier: precision recall f1-score support 良性 0.96 0.99 0.98 103 恶性 0.98 0.94 0.96 68 accuracy 0.97 171 macro avg 0.97 0.97 0.97 171 weighted avg 0.97 0.97 0.97 171 precision&recall&f1-score of SGD Classifier: precision recall f1-score support 良性 0.97 0.99 0.98 103 恶性 0.98 0.96 0.97 68 accuracy 0.98 171 macro avg 0.98 0.97 0.98 171 weighted avg 0.98 0.98 0.98 171 |
显然这里Logistic回归准确率为97%略低于随机梯度参数估计98%,这与书中说的 “Scikit-learn中采用解析的方式精确计算LogisticRegression参数,而使用梯度估计法估计SGDClassifier的参数,因而LogisticRegression会比SGDClassifier表现出更高的准确性”有所出入,我的理解是数据量还太少不足以说明问题?
| Logistic回归与随机梯度参数估计两种模型预测结果的混淆矩阵,横轴为真实值,纵轴为预测值: LR混淆矩阵: 良性 恶性 良性 102 1 恶性 4 64 SgdC混淆矩阵: 良性 恶性 良性 102 1 恶性 3 65 |
支持向量机(分类)
支持向量机也是一个经典的二分类模型,它旨在给定的数据中找到一个超平面,这个超平面在将不同类别的样本分割开时,要保证距离它最近数据点几何距离最大,即表现出更强的鲁棒性,这些用来真正帮助决策最优线性分类模型的数据点叫做“支持向量”。
这一节使用支持向量机来对邮局信件上的收信人邮编进行识别和分类,一遍确定信件的投送地。手写体数字图片数据集集成在Scikit-learn内部,共1797组数据,每幅图片有8*8=64个像素点,即每组数据有64个数字,这些像素矩阵会被逐行首尾连接成一个数组。另外这个分类任务其实是个多分类,在后面会做具体说明,代码如下:
import pandas as pd
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
# 加载手写体数字的数码图像数据
digits = load_digits()
print(digits.data.shape)
print(digits.data[0, :])
# 分割训练集和测试集 3:1
x_train, x_test, y_train, y_test = train_test_split(
digits.data, digits.target, test_size=0.25, random_state=22)
# 数据标准化
ss = StandardScaler()
x_train = ss.fit_transform(x_train)
x_test = ss.fit_transform(x_test)
# 初始化线性假设的支持向量机分类器
linSvc = LinearSVC()
# 进行模型训练
linSvc.fit(x_train, y_train)
# 利用训练好的模型对测试样本的数字类别进行预估
y_predict = linSvc.predict(x_test)
# 准确性测评
print('The Accuracy of Linear SVC is'), linSvc.score(x_test, y_test)
# 对预测结果做更详细的分析
print('precision&recall&f1-score of Linear SVC:', '\n',
classification_report(y_test, y_predict,
target_names=digits.target_names.astype(str)))
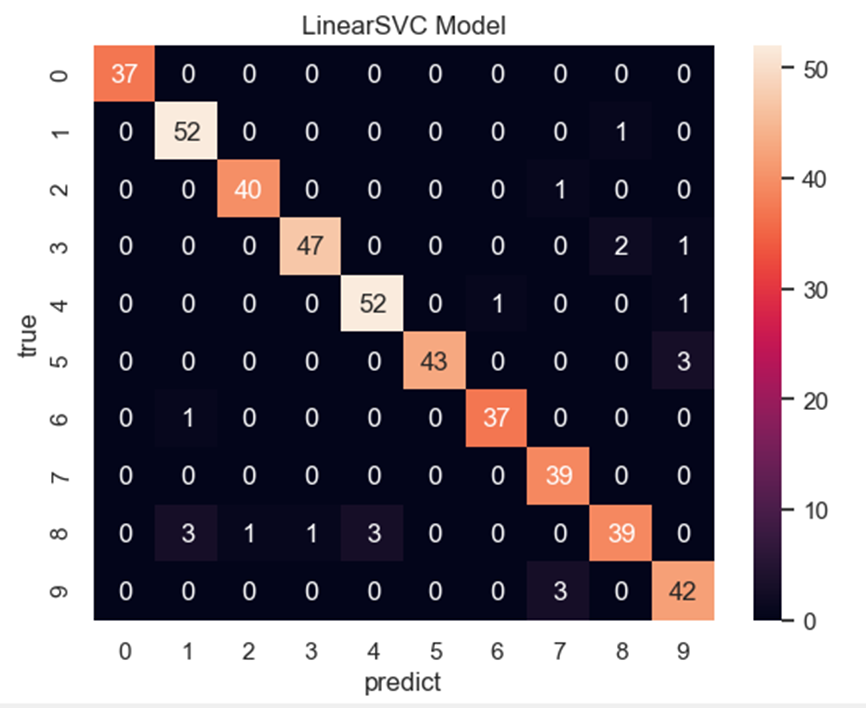
# 求取两种模型预测结果的混淆矩阵
cmSVC = pd.DataFrame(confusion_matrix(y_test, y_predict),
index=digits.target_names.astype(str),
columns=digits.target_names.astype(str))
print('LR混淆矩阵:', '\n', cmSVC)
# 设置Seaborn绘图风格默认
sns.set()
plt.figure(1)
sns.heatmap(cmSVC, annot=True, fmt="d",
xticklabels=digits.target_names.astype(str),
yticklabels=digits.target_names.astype(str))
plt.xlabel('predict'), plt.ylabel('true'), plt.title('Logistic Model')
plt.show()同样的,除了混淆矩阵部分是我自己加的,其他部分基本与书上一致。这里也没有什么新的地方需要解释,就说一点,按书中代码不做任何修改的话,在训练模型时会报警告:{ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.warnings.warn(“Liblinear failed to converge, increase “)。这里是因为支持向量机分类器LinearSVC算法默认的最大迭代次数max_iter是1000,将其改大一点就可以正常运行了,比如3000,算法介绍及修改具体见_classes.py文件。
| 显示第一组数据: (1797, 64) [ 0. 0. 5. 13. 9. 1. 0. 0. 0. 0. 13. 15. 10. 15. 5. 0. 0. 3. 15. 2. 0. 11. 8. 0. 0. 4. 12. 0. 0. 8. 8. 0. 0. 5. 8. 0. 0. 9. 8. 0. 0. 4. 11. 0. 1. 12. 7. 0. 0. 2. 14. 5. 10. 12. 0. 0. 0. 0. 6. 13. 10. 0. 0. 0.] 可以看出每组数据的确是64个像素点数据,后面的点应该是表示浮点类型。 支持向量机预测的准确性: The Accuracy of Linear SVC is 0.9511111111111111 支持向量机模型精确率&召回率&F1指标参数: precision&recall&f1-score of Linear SVC: precision recall f1-score support 0 1.00 1.00 1.00 37 1 0.93 0.98 0.95 53 2 0.98 0.98 0.98 41 3 0.98 0.94 0.96 50 4 0.95 0.96 0.95 54 5 1.00 0.93 0.97 46 6 0.97 0.97 0.97 38 7 0.91 1.00 0.95 39 8 0.93 0.83 0.88 47 9 0.89 0.93 0.91 45 accuracy 0.95 450 macro avg 0.95 0.95 0.95 450 weighted avg 0.95 0.95 0.95 450 |
可以看出这里有0~9是个分类类别,具体指什么书中没讲,我个人理解是:十个地点,比如0代表北京,9代表安徽之类?仅供参考。算法是将当前所要预测的类别作为阴性样本,其他9组均视为阳性样本,这样就是一个二分类任务了,以此类推实现了十分类。
| 支持向量机模型模型预测结果的混淆矩阵,横轴为真实值,纵轴为预测值: SVM混淆矩阵: 0 1 2 3 4 5 6 7 8 9 0 37 0 0 0 0 0 0 0 0 0 1 0 52 0 0 0 0 0 0 1 0 2 0 0 40 0 0 0 0 1 0 0 3 0 0 0 47 0 0 0 0 2 1 4 0 0 0 0 52 0 1 0 0 1 5 0 0 0 0 0 43 0 0 0 3 6 0 1 0 0 0 0 37 0 0 0 7 0 0 0 0 0 0 0 39 0 0 8 0 3 1 1 3 0 0 0 39 0 9 0 0 0 0 0 0 0 3 0 42 |
可以看出整体预测效果都还不错,1389略差些
朴素贝叶斯
贝叶斯分类器是一种基于概率框架的经典统计学习算法,依据贝叶斯决策论知道要最小化分类错误率,即要求对于一个特定的样本x,得到某一类别c下的最大后验概率P(c|x),通过贝叶斯公式转化为,根据训练样本来估计先验概率P(c)和类条件概率P(x|c),但是类条件概率P(x|c)是所有属性上的联合概率,难以从有限的训练样本直接估计得到,一种常用策略是先假定这个类条件概率服从某个确定的概率分布,再基于训练样本对这个分布的未知2参数进行极大似然估计得到,这个方法的缺陷在于若一开始的概率分布假设远离实际数据模型,就会产生误导性预测结果。
为了避开上面这个问题,朴素贝叶斯分类器假设每个维度的特征被分类的条件概率之间是相互独立的,这样一来,训练过程就变成了通过训练数据来估计先验概率P(c)和每个属性的条件概率P(xi|c)。其中有个问题,若训练样本中有某个属性没有和哪个类同时出现过,那么不论其他属性如何支持这个类也会被否定掉,为了避免其他属性携带的信息被这个未出现的属性“抹去”,在估计概率值时通常要进行“拉普拉斯修正”。这一段理解主要参考《机器学习》(西瓜书)。
本节将使用朴素贝叶斯实现对18846条新闻的20分类,代码如下:
import pandas as pd
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
news = fetch_20newsgroups(subset='all')
print(len(news.data), '\n', news.data[0])
# 分割训练集和测试集 3:1
x_train, x_test, y_train, y_test = train_test_split(
news.data, news.target, test_size=0.25, random_state=23)
# 将文本转化为特征向量
vec = CountVectorizer()
x_train = vec.fit_transform(x_train)
x_test = vec.transform(x_test)
# 使用默认配置初始化朴素贝叶斯模型
mnb = MultinomialNB()
# 利用训练集对模型参数进行估计
mnb.fit(x_train, y_train)
# 对测试样本进行类别预测
y_predict = mnb.predict(x_test)
# 准确性测评
print('The Accuracy of Linear Naive Bayes is', mnb.score(x_test, y_test))
# 对预测结果做详细分析
print('precision&recall&f1-score of Linear Naive:', '\n',
classification_report(y_test, y_predict,
target_names=news.target_names))
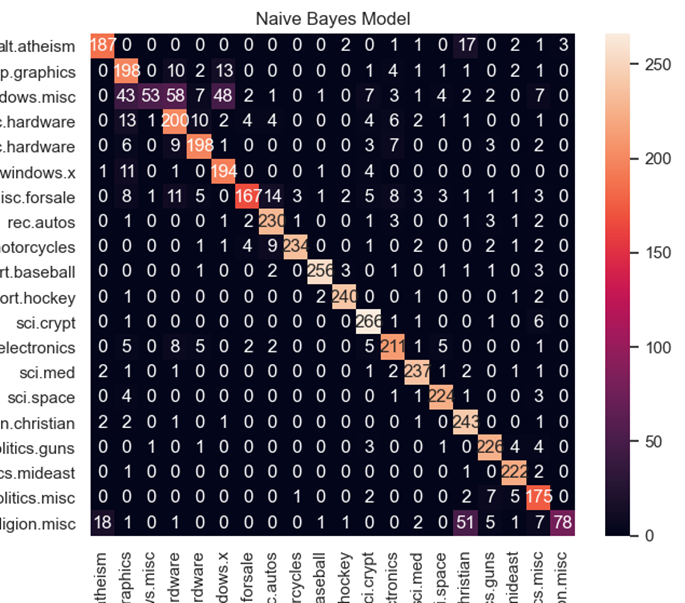
# 求取两种模型预测结果的混淆矩阵
cmMnb = pd.DataFrame(confusion_matrix(y_test, y_predict),
index=news.target_names,
columns=news.target_names)
print('Naive Bayes混淆矩阵:', '\n', cmMnb)
# 设置Seaborn绘图风格默认
sns.set()
plt.figure(1)
sns.heatmap(cmMnb, annot=True, fmt="d",
xticklabels=news.target_names,
yticklabels=news.target_names)
plt.xlabel('predict'), plt.ylabel('true'), plt.title('Naive Bayes Model')
plt.show()| 数据集长度及第一组数据内容: 18846 From: Mamatha Devineni Ratnam <mr47+@andrew.cmu.edu> Subject: Pens fans reactions Organization: Post Office, Carnegie Mellon, Pittsburgh, PA Lines: 12 NNTP-Posting-Host: po4.andrew.cmu.edu I am sure some bashers of Pens fans are pretty confused about the lack of any kind of posts about the recent Pens massacre of the Devils. Actually, I am bit puzzled too and a bit relieved. However, I am going to put an end to non-PIttsburghers’ relief with a bit of praise for the Pens. Man, they are killing those Devils worse than I thought. Jagr just showed you why he is much better than his regular season stats. He is also a lot fo fun to watch in the playoffs. Bowman should let JAgr have a lot of fun in the next couple of games since the Pens are going to beat the pulp out of Jersey anyway. I was very disappointed not to see the Islanders lose the final regular season game. PENS RULE!!! 朴素贝叶斯模型准确率&精确率&召回率&F1指标参数: The Accuracy of Linear Naive Bayes is 0.8571731748726655 precision&recall&f1-score of Linear Naive: precision recall f1-score support alt.atheism 0.89 0.87 0.88 214 comp.graphics 0.67 0.85 0.75 234 comp.os.ms-windows.misc 0.95 0.22 0.36 239 comp.sys.ibm.pc.hardware 0.67 0.80 0.73 249 comp.sys.mac.hardware 0.86 0.86 0.86 229 comp.windows.x 0.74 0.92 0.82 212 misc.forsale 0.92 0.70 0.80 237 rec.autos 0.88 0.93 0.91 246 rec.motorcycles 0.98 0.91 0.94 257 rec.sport.baseball 0.98 0.95 0.96 269 rec.sport.hockey 0.97 0.97 0.97 247 sci.crypt 0.88 0.96 0.92 276 sci.electronics 0.85 0.86 0.86 245 sci.med 0.93 0.95 0.94 249 sci.space 0.93 0.96 0.94 234 soc.religion.christian 0.75 0.97 0.85 251 talk.politics.guns 0.90 0.94 0.92 240 talk.politics.mideast 0.92 0.98 0.95 226 talk.politics.misc 0.78 0.91 0.84 192 talk.religion.misc 0.96 0.47 0.63 166 accuracy 0.86 4712 macro avg 0.87 0.85 0.84 4712 weighted avg 0.87 0.86 0.85 4712 朴素贝叶斯模型预测结果的混淆矩阵,横轴为真实值,纵轴为预测值: Naive Bayes混淆矩阵: alt.atheism … talk.religion.misc alt.atheism 187 … 3 comp.graphics 0 … 0 comp.os.ms-windows.misc 0 … 0 comp.sys.ibm.pc.hardware 0 … 0 comp.sys.mac.hardware 0 … 0 comp.windows.x 1 … 0 misc.forsale 0 … 0 rec.autos 0 … 0 rec.motorcycles 0 … 0 rec.sport.baseball 0 … 0 rec.sport.hockey 0 … 0 sci.crypt 0 … 0 sci.electronics 0 … 0 sci.med 2 … 0 sci.space 0 … 0 soc.religion.christian 2 … 0 talk.politics.guns 0 … 0 talk.politics.mideast 0 … 0 talk.politics.misc 0 … 0 talk.religion.misc 18 … 78 |
害,这不分析了跟前面都差不多,没啥意思,主要理解分类原理。朴素贝叶斯模型被广泛应用于海量互联网文本分类任务,前提假设是条件独立,极大减少了估计参数的规模,节约了算力,同时也抹去了不同特征之间的联系,导致分类性能表现一般。
K近邻(分类)
K近邻模型算法很容易直观理解,对于一个已经做好分类标记的数据集,分布在特征空间中,当其中一个样本分类未知时,模型以在特征空间中的几何距离最近的K个样本为参考,这K个样本中,归属哪个类的样本最多,就将这个未知的样本标记为该类。显然K的取值不同,会得到不同效果的分类器。这一节利用K近邻算法对鸢尾物种进行分类,鸢尾数据集与之前的手写邮编数据集一样集成在Scikit-learn的工具包中,分类代码如下:
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
# 导入数据
iris = load_iris()
print(iris.data.shape)
print(iris.DESCR)
# 分割训练集和测试集 3:1
x_train, x_test, y_train, y_test = train_test_split(
iris.data, iris.target, test_size=0.25, random_state=24)
# 数据标准化
ss = StandardScaler()
x_train = ss.fit_transform(x_train)
x_test = ss.fit_transform(x_test)
# 训练K邻近模型,预测测试集
knc = KNeighborsClassifier()
knc.fit(x_train, y_train)
y_predict = knc.predict(x_test)
# 准确性测评
print('The Accuracy of K-Nearest Neighbor Classifier is', knc.score(x_test, y_test))
# 对预测结果做更详细的分析
print('precision&recall&f1-score of K-Nearest Neighbor Classifier:', '\n',
classification_report(y_test, y_predict,
target_names=iris.target_names))
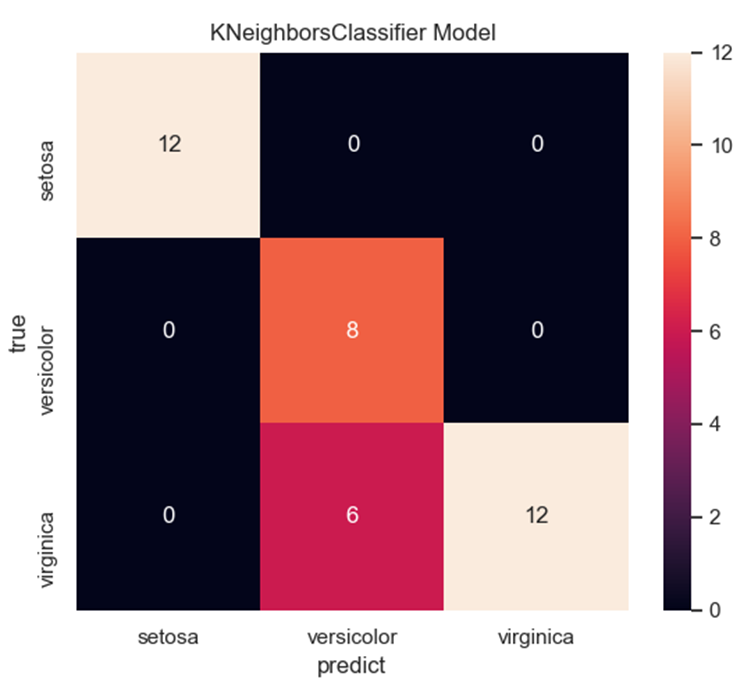
# 求取K邻近模型预测结果的混淆矩阵
cmKnc = pd.DataFrame(confusion_matrix(y_test, y_predict),
index=iris.target_names,
columns=iris.target_names)
print('KNeighborsClassifier混淆矩阵:', '\n', cmKnc)
# 设置Seaborn绘图风格默认
sns.set()
plt.figure(1)
sns.heatmap(cmKnc, annot=True, fmt="d",
xticklabels=iris.target_names,
yticklabels=iris.target_names)
plt.xlabel('predict'), plt.ylabel('true'), plt.title('KNeighborsClassifier Model')
plt.show()| 数据规模和数据说明: (150, 4) :Number of Instances: 150 (50 in each of three classes) :Number of Attributes: 4 numeric, predictive attributes and the class :Attribute Information: – sepal length in cm – sepal width in cm – petal length in cm – petal width in cm – class: – Iris-Setosa – Iris-Versicolour – Iris-Virginica |
可以看出该鸢尾数据集共有150组数据样本,均匀分布在3个不同的亚种,分别是Setosa、Versicolour、Virginica,有4个特征,分别是花瓣、花萼的长度和宽度。
| K分类模型准确率&精确率&召回率&F1指标参数: The Accuracy of K-Nearest Neighbor Classifier is 0.8421052631578947 precision&recall&f1-score of K-Nearest Neighbor Classifier: precision recall f1-score support setosa 1.00 1.00 1.00 12 versicolor 0.57 1.00 0.73 8 virginica 1.00 0.67 0.80 18 accuracy 0.84 38 macro avg 0.86 0.89 0.84 38 weighted avg 0.91 0.84 0.85 38 这里可以看出对Versicolour和Virginica这两个类别识别效果比较糟糕 K分类模型预测结果的混淆矩阵,横轴为真实值,纵轴为预测值: KNeighborsClassifier混淆矩阵: setosa versicolor virginica setosa 12 0 0 versicolor 0 8 0 virginica 0 6 12 |
从混淆矩阵就更直观可以看出Versicolour和Virginica两个类别经常被互相错误识别。
K邻近模型没有使用任何学习算法分析训练数据,属于无参数模型中非常简单的一种。该模型处理一个样本,都需要对预先加载在内存的训练样本进行遍历加上一系列相关计算,算法复杂度是平方级的,随着数据规模增大,会消耗更多的内存和算力。
决策树&2.1.1.6集成模型
决策树不同于Logistic回归和支持向量机,它是用于描述非线性关系的。决策树节点代表数据特征,每个节点下的分支代表对应特征值分类,叶子节点显示模型的决策结果。显然不同特征组合会得到不同的结构分支,从而影响决策树的性能。集成模型中随机森林分类器利用相同训练数据同时搭建多个独立的决策树模型,放弃了单一标准决策树根据每维特征对预测结果影响程度的排序算法,转为随机选取特征;梯度提升决策树则是按照一定次序搭建多个决策树模型,这些模型之间存在彼此依赖关系,每一个后续模型的加入都会提升现有模型的综合性能。
这两节使用泰坦尼克号的乘客数据来检测单一决策树、随机森林分类器和梯度提升决策树的性能差异。分类任务为根据乘客的某些特征来预测该乘客是否生还,代码如下:
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
# 加载数据集
titanic = pd.read_csv('titanic.txt')
print(titanic.head())
print(titanic.info())
# 人工选取pclass、age以及sex作为判别乘客是否能够生还的特征
x = titanic[['pclass', 'age', 'sex']]
y = titanic['survived']
# 数据预处理,对age特征缺失的数据使用平均值代替
x['age'].fillna(x['age'].mean(), inplace=True)
# 分割训练集和测试集 3:1
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.25, random_state=25)
# 对类别型特征进行转化,成为特征向量
vec = DictVectorizer(sparse=False)
x_train = vec.fit_transform(x_train.to_dict(orient='records'))
x_test = vec.fit_transform(x_test.to_dict(orient='records'))
print(vec.feature_names_)
# 使用单一决策树进行训练及预测
dtc = DecisionTreeClassifier()
dtc.fit(x_train, y_train)
dtc_y_pred = dtc.predict(x_test)
# 使用随机森林分类器训练及预测
rfc = RandomForestClassifier()
rfc.fit(x_train, y_train)
rfc_y_pred = rfc.predict(x_test)
# 使用梯度提升决策树进行训练及预测
gbc = GradientBoostingClassifier()
gbc.fit(x_train, y_train)
gbc_y_pred = gbc.predict(x_test)
# 三种模型对泰坦尼克号数据预测性能
# 准确性测评
print('The Accuracy of DecisionTree&RandomForestClassifier&GradientTreeBoosting is', '\n',
dtc.score(x_test, y_test), '\n',
rfc.score(x_test, y_test), '\n',
gbc.score(x_test, y_test))
# 对预测结果做更详细的分析
print('precision&recall&f1-score of '
'DecisionTree&RandomForestClassifier&GradientTreeBoosting:', '\n',
classification_report(y_test, dtc_y_pred, target_names=['died', 'survived']), '\n',
classification_report(y_test, rfc_y_pred, target_names=['died', 'survived']), '\n',
classification_report(y_test, gbc_y_pred, target_names=['died', 'survived']))
# 求取三个模型预测结果的混淆矩阵
cmDtc = pd.DataFrame(confusion_matrix(y_test, dtc_y_pred),
index=['died', 'survived'],
columns=['died', 'survived'])
cmRfc = pd.DataFrame(confusion_matrix(y_test, rfc_y_pred),
index=['died', 'survived'],
columns=['died', 'survived'])
cmGbc = pd.DataFrame(confusion_matrix(y_test, gbc_y_pred),
index=['died', 'survived'],
columns=['died', 'survived'])
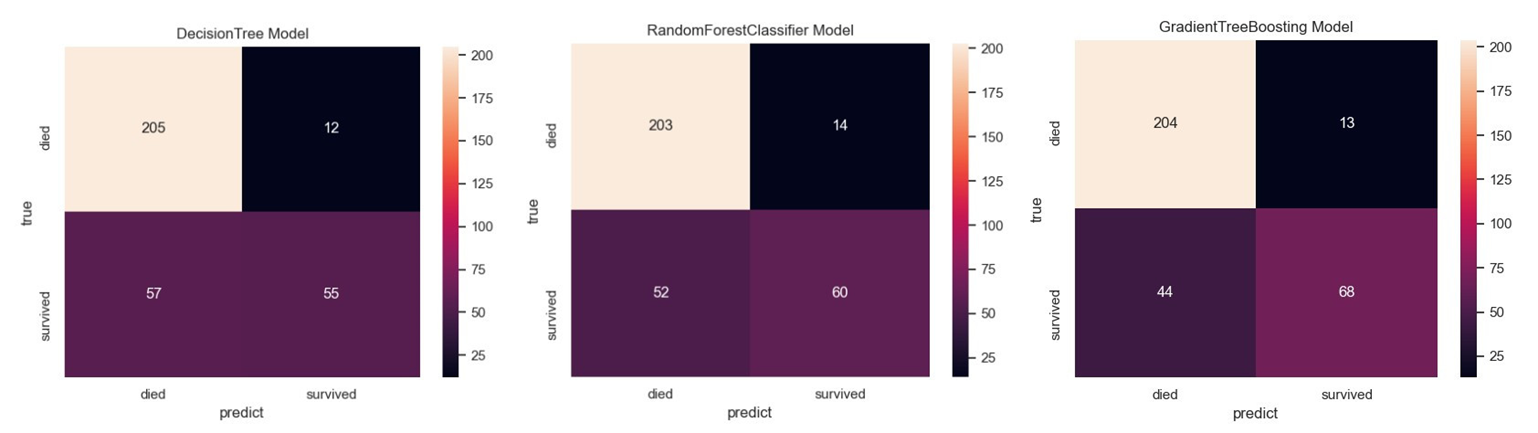
print('DecisionTree混淆矩阵:', '\n', cmDtc, '\n',
'RandomForestClassifier混淆矩阵:', '\n', cmRfc, '\n',
'GradientTreeBoosting混淆矩阵:', '\n', cmGbc)
# 设置Seaborn绘图风格默认
sns.set()
plt.figure(1)
sns.heatmap(cmDtc, annot=True, fmt="d",
xticklabels=['died', 'survived'],
yticklabels=['died', 'survived'])
plt.xlabel('predict'), plt.ylabel('true'), plt.title('DecisionTree Model')
plt.figure(2)
sns.heatmap(cmRfc, annot=True, fmt="d",
xticklabels=['died', 'survived'],
yticklabels=['died', 'survived'])
plt.xlabel('predict'), plt.ylabel('true'), plt.title('RandomForestClassifier Model')
plt.figure(3)
sns.heatmap(cmGbc, annot=True, fmt="d",
xticklabels=['died', 'survived'],
yticklabels=['died', 'survived'])
plt.xlabel('predict'), plt.ylabel('true'), plt.title('GradientTreeBoosting Model')
plt.show()| 查看数据的统计特性: [5 rows x 11 columns] <class ‘pandas.core.frame.DataFrame’> RangeIndex: 1313 entries, 0 to 1312 Data columns (total 11 columns): # Column Non-Null Count Dtype — —— ————– —– 0 row.names 1313 non-null int64 1 pclass 1313 non-null object 2 survived 1313 non-null int64 3 name 1313 non-null object 4 age 633 non-null float64 5 embarked 821 non-null object 6 home.dest 754 non-null object 7 room 77 non-null object 8 ticket 69 non-null object 9 boat 347 non-null object 10 sex 1313 non-null object dtypes: float64(1), int64(2), object(8) |
数据说明有1313条乘客信息,其中有部分特征数据有缺失,数据类型也不尽相同,所以在训练之前要做预处理
| 选取pclass、age以及sex特征,用平均值补全缺失的参数: [‘age’, ‘pclass=1st’, ‘pclass=2nd’, ‘pclass=3rd’, ‘sex=female’, ‘sex=male’] |
预处理后得到共有六条特征,因为sex和palass两个数据列是类别型的,转换特征后,每个类别型的特征都将或独成一列特征,类似字典
对于填补缺失值数据,执行语句x[‘age’].fillna(x[‘age’].mean(), inplace=True)会报出警告:SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame,也找过解决方案,但网上的帖子基本都是复制转载,是不是对的还不可知,主要思想是使用行列索引直接赋值,但如果说之前访问的是副本,它最后还是修改了原数据内存,不太理解这样还有警报,这里不影响结果,先放着
| 三种模型的准确率和precision&recall&f1-score性能指标 The Accuracy of DecisionTree&RandomForestClassifier&GradientTreeBoosting is 0.790273556231003 0.7993920972644377 0.8267477203647416 precision&recall&f1-score of DecisionTree&RandomForestClassifier&GradientTreeBoosting: precision recall f1-score support died 0.78 0.94 0.86 217 survived 0.82 0.49 0.61 112 accuracy 0.79 329 macro avg 0.80 0.72 0.74 329 weighted avg 0.80 0.79 0.77 329 precision recall f1-score support died 0.80 0.94 0.86 217 survived 0.81 0.54 0.65 112 accuracy 0.80 329 macro avg 0.80 0.74 0.75 329 weighted avg 0.80 0.80 0.79 329 precision recall f1-score support died 0.82 0.94 0.88 217 survived 0.84 0.61 0.70 112 accuracy 0.83 329 macro avg 0.83 0.77 0.79 329 weighted avg 0.83 0.83 0.82 329 很明显性能排名是:单一决策树、随机森林分类器和梯度提升决策树依次递增 三种模型的混淆矩阵: DecisionTree混淆矩阵: died survived died 205 12 survived 57 55 RandomForestClassifier混淆矩阵: died survived died 203 14 survived 52 60 GradientTreeBoosting混淆矩阵: died survived died 204 13 survived 44 68 |
输出表明,三种模型在遇难者方面性能较好,在生还预测方面则较差。
回归预测
回归不同于分类,面向的是连续变量。这一节都是针对“美国波士顿地区房价预测”这一个回归问题进行对比分析,用到的模型在前面也已经都提过了,这一节我只做前面线性回归和支持向量机回归两个实例,并且放在一起,从这里开始也不会像前面那样细致说明了。
在回归问题中,优化目标是最小化预测结果和真实值之间的差异。对于线性回归采用LinearRegression和SGDRegressor两种模型分别进行训练预测,并作出评价比较。支持向量机模型这次采用了三种不同的核函数修改了默认配置,最后作出评价比较,核函数用于提供某种算法变换,可以将分布在线性不可分低维度的数据映射到高维可分的特征空间,比如二维平面中的两个同心圆是无法用一条直线分割开的,但是映射到三维空间,使得两个圆在其法线上存在空间距离,就可以被一个平面分隔开了,不禁想起了三体中的降维打击。这套波士顿房价数据共有506条,包含对房屋的13项数值型特征描述和目标房价,无数据与属性缺失,回归预测代码如下:
import numpy as np
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
boston = load_boston()
x = boston.data
y = boston.target
x_train, x_test, y_train, y_test = train_test_split(x, y,
test_size=0.25,
random_state=33)
print('The max target value is', np.max(boston.target), '\n',
'The min target value is', np.min(boston.target), '\n',
'The average target value is', np.mean(boston.target))
# 预测目标房价之间的差异较大,对特征和目标值进行标准化处理(可还原真实结果)
ss_x = StandardScaler()
ss_y = StandardScaler()
x_train = ss_x.fit_transform(x_train)
x_test = ss_x.transform(x_test)
y_train = ss_y.fit_transform(y_train.reshape(-1, 1))
y_test = ss_y.transform(y_test.reshape(-1, 1))
'''线性回归器'''
# 使用线性回归模型LinearRegression和SGDRegressor分别对波士顿房价数据进行训练学习及预测
lr = LinearRegression()
lr.fit(x_train, y_train)
lr_y_predict = lr.predict(x_test)
sgdr = SGDRegressor()
sgdr.fit(x_train, y_train)
sgdr_y_predict = sgdr.predict(x_test)
# 评价LinearRegression和SGDRegressor两种模型性能
# LinearRegression模型自带评估模块、R2、MSE均方误差和MAE平均绝对误差的评估结果
print('The value of default measurement of LinearRegression is',
lr.score(x_test, y_test), '\n',
'The value of R-squared of LinearRegression is',
r2_score(y_test, lr_y_predict), '\n',
'The mean squared error of LinearRegression is',
mean_squared_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(lr_y_predict)), '\n',
'The mean absoluate error of LinearRegression is',
mean_absolute_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(lr_y_predict))
)
# SGDRegressor模型自带评估模块、R2、MSE均方误差和MAE平均绝对误差评估结果
print('The value of default measurement of SGDRegressor is',
sgdr.score(x_test, y_test), '\n',
'The value of R-squared of SGDRegressor is',
r2_score(y_test, sgdr_y_predict), '\n',
'The mean squared error of SGDRegressor is',
mean_squared_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(sgdr_y_predict)), '\n',
'The mean absoluate error of SGDRegressor is',
mean_absolute_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(sgdr_y_predict))
)
'''支持向量机(回归)
from sklearn.svm import SVR
# 使用线性核函数配置的支持向量机进行回归训练和预测
linear_svr = SVR(kernel='linear')
linear_svr.fit(x_train, y_train)
linear_svr_y_predict = linear_svr.predict(x_test)
# 使用多项式核函数配置的支持向量机进行回归训练和预测
poly_svr = SVR(kernel='poly')
poly_svr.fit(x_train, y_train)
poly_svr_y_predict = poly_svr.predict(x_test)
# 使用径向基核函数配置的支持向量机进行回归训练和预测
rbf_svr = SVR(kernel='rbf')
rbf_svr.fit(x_train, y_train)
rbf_svr_y_predict = rbf_svr.predict(x_test)
# 使用R2、MSE均方误差和MAE平均绝对误差对三种配置支持向量机(回归)模型在相同测试集上进行性能评估
print('The value of R-squared of Linear SVR is',
linear_svr.score(x_test, y_test), '\n',
'The mean squared error of Linear SVR is',
mean_squared_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(linear_svr_y_predict)), '\n',
'The mean absoluate error of Linear SVR is',
mean_absolute_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(linear_svr_y_predict))
)
print('The value of R-squared of poly SVR is',
poly_svr.score(x_test, y_test), '\n',
'The mean squared error of poly SVR is',
mean_squared_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(poly_svr_y_predict)), '\n',
'The mean absoluate error of poly SVR is',
mean_absolute_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(poly_svr_y_predict))
)
print('The value of R-squared of rbf SVR is',
rbf_svr.score(x_test, y_test), '\n',
'The mean squared error of rbf SVR is',
mean_squared_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(rbf_svr_y_predict)), '\n',
'The mean absoluate error of rbf SVR is',
mean_absolute_error(ss_y.inverse_transform(y_test),
ss_y.inverse_transform(rbf_svr_y_predict))
)
'''两种模型训练后需要对其做性能评测,来衡量预测值与真实值之间的差距,最直观的评价指标包括平均绝对误差MAE和均方误差MSE,这也是线性回归模型的优化目标,但用相同的模型来预测不同的问题以上两个指标也可能相差甚远,因此需要一个具备统计学含义的评价指标,这里引入了R-aquared用来衡量模型回归结果的波动可被真实值验证的百分比,暗示了模型在数值回归方面的能力。
| 截取线性回归运行结果: The value of default measurement of LinearRegression is 0.675795501452948 The value of R-squared of LinearRegression is 0.675795501452948 The mean squared error of LinearRegression is 25.139236520353457 The mean absoluate error of LinearRegression is 3.5325325437053983 The value of default measurement of SGDRegressor is 0.6713363955638852 The value of R-squared of SGDRegressor is 0.6713363955638852 The mean squared error of SGDRegressor is 25.485001363583066 The mean absoluate error of SGDRegressor is 3.496855077386283 |
从结果可知,模型自带的评估模块与使用r2_score函数是等价的,从两种模型的比较来看,LinearRegression要优于随机梯度下降估计参数的方法SGDRegressor,书中另指出,当预测任务规模很大超过十万时,推荐随机梯度下降法。支持向量机的预测结果就不贴出来了,最后结果与书中一致,径向基核函数对特征进行非线性映射,展现出回归性能最佳。
K邻近和回归树简单提下,不贴代码了。此处的K邻近模型还是借助周围K个最近训练样本的目标数值,对待测样本的回归值进行决策,采用了对K个邻近目标数值的算术平均法和考虑距离的加权平均两种配置,显然加权平均的效果会好些,结果也证实了。回归树选择不同特征作为分裂节点,叶节点则是一个个具体的值,树模型特点有:1.处理非线性特征问题;2.不要求特征标准化和统一量化,即兼容数值型和类别型特征。树模型缺点有:1.模型搭建过于复杂,缺乏对新数据预测精度,即过拟合,泛化力弱;2.细微的数据更改可能导致模型结构发生较大变化,稳定性较差;3.无法在有限时间找到最优解,常借助集成模型,在多个次优解中寻觅更高的模型性能。
无监督学习经典模型
无监督学习重在发现数据本身的特点,不需要对数据进行标记,从功能角度看,无监督学习可以用来做数据聚类和特征降维。
数据聚类(K均值算法)
这一小节使用K均值(K-means)算法来做数据聚类,算法要求随机预设好聚类的个数,根据每个数据的特征向量,对其进行归属划分,当所有数据都被标记过聚类中心后,计算所有数据点到所属聚类中心距离的平方和,迭代更新聚类中心,直到所有数据点所属的聚类中心与上一次分配的类簇没有变化,即平方和趋于稳定,停止迭代,聚类成功。
本小节使用前面提到的手写体数字图像数据的完整版本举例,数据有两个集合,其中训练样本数据3823条,测试数据1797条,图像数据通过8*8的像素矩阵表示,即共有64个特征维度,一个目标维度表示图像所属类别。我们查看数据就可以知道,图像样本类别共有十个,在前面分类处我猜测是地区,所以这里预设K值也是十个,运行结果聚类准确性约为66%,贴出代码,但不做演示分析。重点说下如何对没有所属类别的数据进行性能评估,在没有了解之前我也很不解,既然都不知道正确答案,如何评判我们做的结果的准确性呢,真的是很佩服前人的智慧,下面是评价指标轮廓系数的演示代码:
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn import metrics
import matplotlib.pyplot as plt
'''K-means算法在手写体数字图像数据上的使用示例'''
'''
# 读取训练集和测试集
digits_train = pd.read_csv('optdigits.tra', header=None)
digits_test = pd.read_csv('optdigits.tes', header=None)
# 分离出64维度像素特征和1维度数字目标
x_train = digits_train[np.arange(64)]
y_train = digits_train[64]
x_test = digits_test[np.arange(64)]
y_test = digits_test[64]
# 初始化KMeans模型,并设置聚类中心数量为10
kmeans = KMeans(n_clusters=10)
kmeans.fit(x_train)
# 逐条判断每个测试图像所属的聚类中心
y_pred = kmeans.predict(x_test)
# 因为该图片数据自身带有正确的类别信息,使用ARI进行K-means聚类性能评估
print('The ARI of KMeans is', metrics.adjusted_rand_score(y_test, y_pred))
'''
'''利用轮廓系数评价不同类簇数量的K-means聚类实例'''
from sklearn.metrics import silhouette_score
plt.figure(1)
plt.subplot(3, 2, 1)
x1 = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
x = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
# 在一号子图做出原始信号点阵分布
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Instances')
plt.scatter(x1, x2)
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'b']
markers = ['o', 's', 'D', 'v', '^', 'p', '*', '+']
clusters = [2, 3, 4, 5, 8]
subplot_counters = 1
sc_scores = []
for t in clusters:
subplot_counters += 1
plt.subplot(3, 2, subplot_counters)
kmeans_model = KMeans(n_clusters=t).fit(x)
print(kmeans_model.labels_)
for i, l in enumerate(kmeans_model.labels_):
plt.plot(x1[i], x2[i], color=colors[l], marker=markers[l], ls='None')
plt.xlim([0, 10])
plt.ylim([0, 10])
sc_score = silhouette_score(x, kmeans_model.labels_,metric='euclidean')
sc_scores.append(sc_score)
plt.title('K=%s, silhouette coefficient=%0.03f' % (t, sc_score))
'''“肘部”观察法示例'''
from scipy.spatial.distance import cdist
cluster1 = np.random.uniform(0.5, 1.5, (2, 10))
cluster2 = np.random.uniform(5.5, 6.5, (2, 10))
cluster3 = np.random.uniform(3.0, 4.0, (2, 10))
# 绘制30个数据样本的分布图像,30行2列
x = np.hstack((cluster1, cluster2, cluster3)).T
plt.figure(2)
plt.subplot(1, 2, 1)
plt.title('Instances')
plt.scatter(x[:, 0], x[:, 1])
plt.xlabel('x1')
plt.ylabel('x2')
# 测试9种不同聚类中心数量下,每组情况的聚类质量
K = range(1, 10)
meandistortions = []
for k in K:
kmeans = KMeans(n_clusters=k)
kmeans.fit(x)
meandistortions.append(sum(np.min(cdist(x, kmeans.cluster_centers_,
'euclidean'), axis=1))/x.shape[0])
plt.subplot(1, 2, 2)
plt.plot(K, meandistortions, 'bx-')
plt.xlabel('k')
plt.ylabel('Average Dispersion')
plt.title('Selecting k with the Elbow Method')
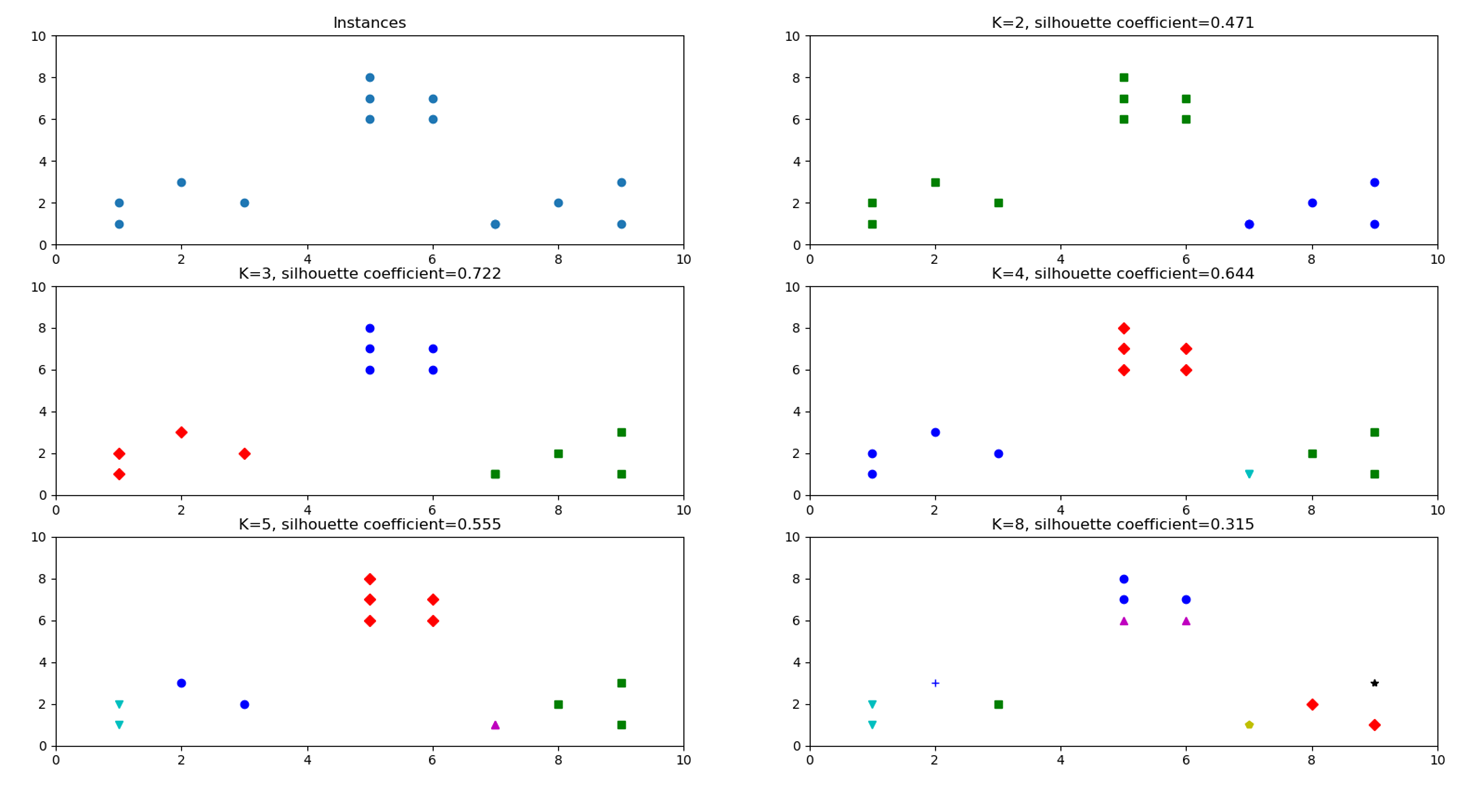
plt.show()轮廓系数取值范围是[-1,1],评价原理也容易理解:对已经聚类好的数据,选定一个类簇中第i个样本Ai,计算Ai与同类簇中其他样本距离的平均值,用于量化簇内的凝聚度;再选定一个Ai外的另一个类簇B,同样计算出Ai与类簇B所有样本的平均距离,遍历所有其他簇,找到最近那个平均距离,用于量化簇之间的分离度,将这些参数代入轮廓系数公式得到轮廓系数,解释到这评价原理就很清楚了,公式就不贴出来了,系数越大越好,小于0则表示聚类效果不好,离其他簇比离本簇还近。运行结果如下:
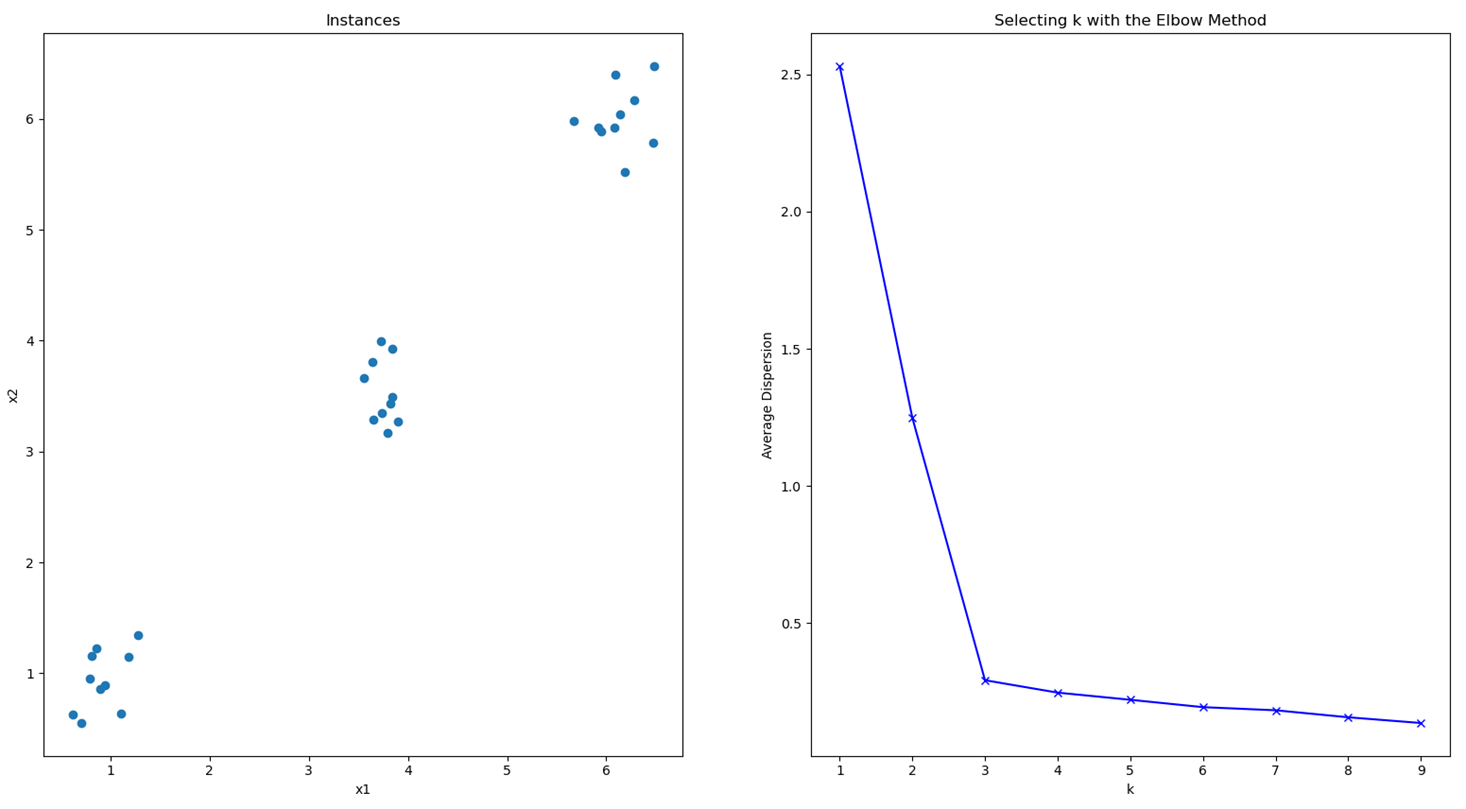
很明显K=3S时轮廓系数最高,也符合原始数据的直观三类。K-means聚类模型采用的迭代式算法,有两个缺陷:1.容易收敛到局部最优解;2.需要预先设定簇的数量。第二点上文说过了,第一点也好理解:经过几次迭代后也是很有可能收敛到几个与真实情况出入很大的聚类,但也确实已经收敛无法迭代更新了,这是算法自身的理论缺陷造成的,可以通过多次执行挑选性能更好的初始中心点。下面针对第二个问题提出了一种“肘部”观察法用于粗略估计相对合理的类簇个数,运行结果如下图:
K-means模型优化目标是所有数据点到各自类簇距离的平方和趋于稳定,所有可以通过观察这个数值随着K的走势来找出最佳类簇数量。增加类簇数量K这个值必然是会减小的,试想如果K值大到接近数据点个数,这个值将会趋于0。上图当K=3时下降速度明显放缓,这表示继续增大K不会有利于算法的收敛了,即K是相对最佳类簇数量。
特征降维(主成分分析)
特征降维是无监督学习的另一个应用,在实际项目中,常会遇到特征维度非常高的样本,无法根据自身现有知识构建有效特征,另外超过三维特征也无法直观感受,特征降维在辅助图像识别方面有突出表现。这一节介绍的主成分分析的运行原理是:对原来的特征空间做映射,使得新的映射后的特征空间数据彼此正交,保留下具备区分性的低维数据特征。这一节沿用上一节手写体数字图像集进行实验,将64个维度压缩到两个维度的特征空间,代码如下:
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
'''K-means算法在手写体数字图像数据上的使用示例'''
# 读取训练集和测试集
digits_train = pd.read_csv('optdigits.tra', header=None)
digits_test = pd.read_csv('optdigits.tes', header=None)
# 分离出64维度像素特征和1维度数字目标
x_digits = digits_train[np.arange(64)]
y_digits = digits_train[64]
# 初始化一个压缩高维至二维的PCA
estimator = PCA(n_components=2)
x_pca = estimator.fit_transform(x_digits)
print(x_pca.shape)
def plot_pca_scatter():
colors = ['black', 'blue', 'purple', 'yellow', 'white',
'red', 'lime', 'cyan', 'orange', 'gray']
for i in range(len(colors)):
px = x_pca[:, 0][y_digits.values == i]
py = x_pca[:, 1][y_digits.values == i]
plt.scatter(px, py, c=colors[i])
plt.legend(np.arange(0, 10).astype(str))
plt.xlabel('First Principal Componpent')
plt.xlabel('Second Principal Componpent')
plt.show()
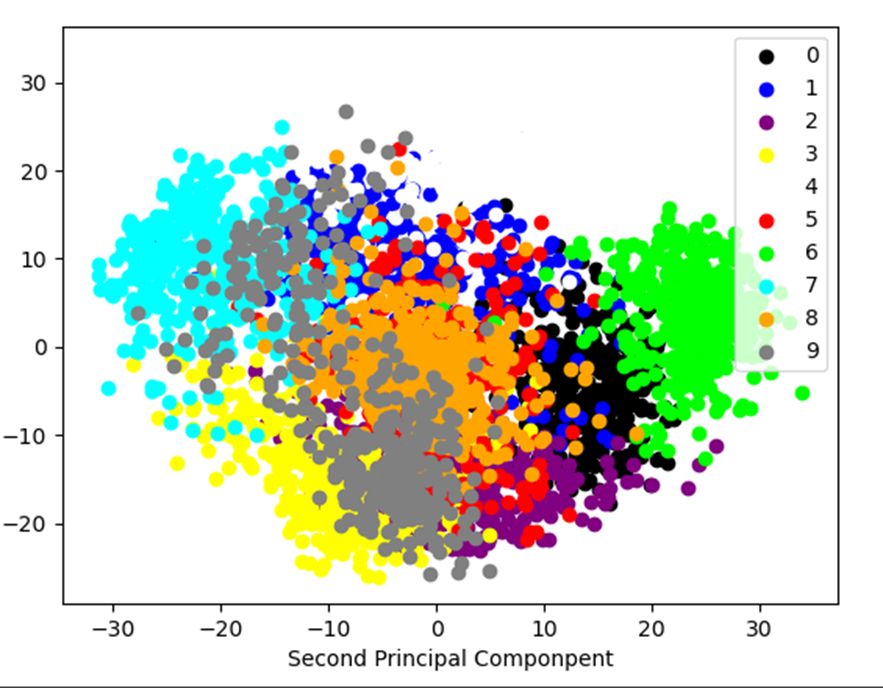
plot_pca_scatter()手写体数字图像经PCA压缩后的二维空间分布
可以观察到大多数数字之间的区分性,书中后面是使用支持向量机来比较降维后的分类效果与原始数据的分类效果,结果是准确性从93%损失到91%。特征降维选取具有代表性的特征,规避大量冗余和噪声,尽管会损失一些有用的模式信息但也节省了用于训练模型的时间。
模型使用技巧
本节介绍了多种提升模型性能的方法,包括如何预处理数据、控制参数训练以及优化模型配置等方法。
特征提升
特征抽取:逐条将数据转化为特征向量的形式,同时包括对数据特征的量化;特征筛选:在特征抽取的基础上,在高维度、已量化的特征向量中选择对指定任务更有效的特征组合。
特征抽取
对于形式为文本的原始数据,需要预先将文本量化为特征向量,下面对一段字典存储的数据进行特征抽取与像量化代码:
# DictVectorizer对使用字典存储的数据进行特征抽取与向量化
from sklearn.feature_extraction import DictVectorizer
# 定义一组字典列表,用来表示多个数据样本(每个字典代表一个数据样本)
measurements = [
{'city': 'Dubai', 'temperature': 33.},
{'city': 'London', 'temperature': 12.},
{'city': 'San Fransisco', 'temperature': 18.}
]
# 初始化DictVectorizer特征提取器
vec = DictVectorizer()
# 输出转化后的特征矩阵
print(vec.fit_transform(measurements).toarray())
# 输出各个维度的特征含义
print(vec.get_feature_names())| 向量化结果: [[ 1. 0. 0. 33.] [ 0. 1. 0. 12.] [ 0. 0. 1. 18.]] [‘city=Dubai’, ‘city=London’, ‘city=San Fransisco’, ‘temperature’] |
对于类别型特征特征向量化,会从原特征中产生新的特征,并采用0/1二值方式进行量化。
对于一些文本数据,常用的文本特征表示方法为词袋法,不考虑词语顺序,将每个出现过的词语视作一个特征,所以不重复词语集合叫做词表。特征数值常见的计算方法有CountVectorizer和TfidfVectorizer,主要区别在于CountVectorizer只统计词语出现频率,TfidfVectorizer同时还会关注词语出现次数的倒数,这对常用词语有着抑制作用,训练文本条数越多优势越明显。另外把每条文本中都会出现的常用词称作停用词,比如the/a等这些对分类没有贡献的词,可以将这些过滤掉以提高性能表现。下面代码是对20类新闻文本问题在去停用词的条件下,使用两种计算特征数值方法的分类:
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
news = fetch_20newsgroups(subset='all')
x_train, x_test, y_train, y_test = train_test_split(
news.data, news.target, test_size=0.25, random_state=33)
# 使用CountVectorizer在去掉停用词的条件下,对文本特征进行量化的朴素贝叶斯分类性能测试
count_vec = CountVectorizer(analyzer='word', stop_words='english')
# 只使用词频统计的方式将训练和测试文本转化为特征向量
x_count_train = count_vec.fit_transform(x_train)
x_count_test = count_vec.transform(x_test)
mnb_count = MultinomialNB()
mnb_count.fit(x_count_train, y_train)
print('The accuracy of classifying 20newsgroups using Naive Bayes'
'(CountVectorizer by filtering stopwords):',
mnb_count.score(x_count_test, y_test))
y_count_predict = mnb_count.predict(x_count_test)
print('precision&recall&f1-score with CountVectorizer:', '\n',
classification_report(y_test, y_count_predict,
target_names=news.target_names))
# 使用TfidfVectorizer在去掉停用词的条件下,对文本特征进行量化的朴素贝叶斯分类性能测试
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vec = TfidfVectorizer(analyzer='word', stop_words='english')
# 使用tfidf的方式将训练和测试文本转化为特征向量
x_tfidf_train = tfidf_vec.fit_transform(x_train)
x_tfidf_test = tfidf_vec.transform(x_test)
mnb_tfidf = MultinomialNB()
mnb_tfidf.fit(x_tfidf_train, y_train)
print('The accuracy of classifying 20newsgroups using Naive Bayes'
'(TfidfTransformer by filtering stopwords):',
mnb_tfidf.score(x_tfidf_test, y_test))
y_tfidf_predict = mnb_tfidf.predict(x_tfidf_test)
print('precision&recall&f1-score with TfidfTransformer:', '\n',
classification_report(y_test, y_tfidf_predict,
target_names=news.target_names))这里我没有写不去掉停用词的部分,也可以稍作改动比较一下,是去掉停用词性能更好。同样的TfidfVectorizer的特征抽取和量化方法更具优势,我这里运行结果是高出两个百分点,结果数据就不贴出来占地方了。
特征筛选
特征筛选的目的也还是更有效的利用数据,但不同于PCA选择主成分对特征进行重建,这样很难解释重建后的特征,特征筛选则是在不修改特征的情况下,寻找出对模型性能提升较大的少量特征。本例使用决策树模型根据Titanic数据集不同区间的特征进行分类,代码如下:
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier
from sklearn import feature_selection
import pylab as pl
# 使用Titanic数据集,通过特征筛选的方法一步步提升决策树的预测性能
titanic = pd.read_csv('titanic.txt')
# 分离数据特征与预测目标
x = titanic.drop(['row.names', 'name', 'survived'], axis=1)
y = titanic['survived']
x['age'].fillna(x['age'].mean(), inplace=True)
x.fillna('UNKNOWN', inplace=True)
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.25, random_state=30)
vec = DictVectorizer()
x_train = vec.fit_transform(x_train.to_dict(orient='records'))
x_test = vec.transform(x_test.to_dict(orient='records'))
print(len(vec.feature_names_))
# 使用决策树模型依靠所有特征进行预测和评估性能
dt = DecisionTreeClassifier(criterion='entropy')
dt.fit(x_train, y_train)
print(dt.score(x_test, y_test))
# 筛选前20%的特征,使用相同配置的决策树进行预测和评估
fs = feature_selection.SelectPercentile(feature_selection.chi2, percentile=20)
x_train_fs = fs.fit_transform(x_train, y_train)
dt.fit(x_train_fs, y_train)
x_test_fs = fs.transform(x_test)
print(dt.score(x_test_fs, y_test))
# 通过交叉验证的方法,按照固定间隔的百分比筛选特征,并作图展示性能随特征筛选比例的变化
percentiles = range(1, 100, 2)
results = []
for i in percentiles:
fs = feature_selection.SelectPercentile(feature_selection.chi2, percentile=i)
x_train_fs = fs.fit_transform(x_train, y_train)
scores = cross_val_score(dt, x_train_fs, y_train, cv=5)
results = np.append(results, scores.mean())
print(results)
opt = np.where(results == results.max())
# 找到体现最佳性能的特征筛选百分比
print('Optimal number of feature %d' % percentiles[opt[0][0]])
print(opt[0][0])
pl.plot(percentiles, results)
pl.xlabel('percentile of feature')
pl.ylabel('accuracy')
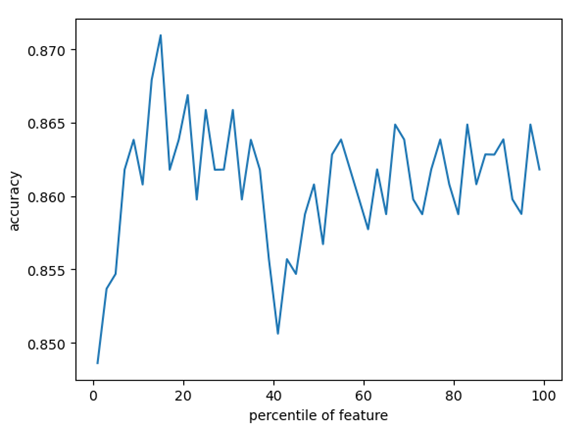
pl.show()程序中分别对全部特征和前20%的特征做了实验,结果表明前20%特征训练测试准确率为87.2%,全部特征的位86%。最后通过循环每次增加2%的特征做训练测试,结果如下图所示:
表明在特征取前15%的时候所取得的性能最好。
模型正则化
正则化的主要目的是为了降低模型复杂度,提升泛化力,在面对测试时表现出更好的性能。
欠拟合与过拟合
拟合是指机器学习模型在训练过程中,通过更新参数,使得模型不断契合训练集的过程。欠拟合是说在训练集和测试集表现的性能都很一般,过拟合是说在训练集表现性能非常好,而在测试集则表现很一般。这一节将构造一个披萨饼尺寸与其对应售价的数据集,分别使用三种回归模型进行训练和测试,代码如下:
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
'''使用线性回归模型在披萨训练样本上进行拟合'''
# 输入样本特征以及目标值,即披萨直径
x_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
regressor = LinearRegression()
regressor.fit(x_train, y_train)
xx = np.linspace(0, 26, 100)
xx = xx.reshape(xx.shape[0], 1)
# 以上述100个数据点作为基准,预测回归直线
yy = regressor.predict(xx)
plt.subplot(1, 3, 1)
plt.scatter(x_train, y_train)
plt1 = plt.plot(xx, yy, label='Degree=1')
plt.axis([0, 25, 0, 25])
plt.xlabel('Diameter of Pizza')
plt.ylabel('Price of Pizza')
plt.title('R-squared(Degree=1): %.3f' % regressor.score(x_train, y_train))
plt.legend(handles=plt1)
'''使用2次多项式回归模型在披萨训练样本上进行拟合'''
from sklearn.preprocessing import PolynomialFeatures
poly2 = PolynomialFeatures(degree=2)
# 映射出2次多项式特征
x_train_poly2 = poly2.fit_transform(x_train)
# 尽管特征维度有提升,但是模型基础仍然是线性模型
regressor_poly2 = LinearRegression()
# 对2次多项式回归模型进行训练
regressor_poly2.fit(x_train_poly2, y_train)
# 从新映射绘图用x轴采样数据
xx_poly2 = poly2.transform(xx)
yy_poly2 = regressor_poly2.predict(xx_poly2)
plt.subplot(1, 3, 2)
plt.scatter(x_train, y_train)
plt1 = plt.plot(xx, yy, label='Degree=1')
plt2 = plt.plot(xx, yy_poly2, label='Degree=2')
plt.axis([0, 25, 0, 25])
plt.xlabel('Diameter of Pizza')
plt.ylabel('Price of Pizza')
plt.title('R-squared(Degree=2): %.3f' % regressor_poly2.score(x_train_poly2, y_train))
plt.legend(handles=plt1+plt2)
'''使用4次多项式回归模型在披萨训练样本上进行拟合'''
poly4 = PolynomialFeatures(degree=4)
x_train_poly4 = poly4.fit_transform(x_train)
regressor_poly4 = LinearRegression()
regressor_poly4.fit(x_train_poly4, y_train)
xx_poly4 = poly4.transform(xx)
yy_poly4 = regressor_poly4.predict(xx_poly4)
plt.subplot(1, 3, 3)
plt.scatter(x_train, y_train)
plt1 = plt.plot(xx, yy, label='Degree=1')
plt2 = plt.plot(xx, yy_poly2, label='Degree=2')
plt4 = plt.plot(xx, yy_poly4, label='Degree=4')
plt.axis([0, 25, 0, 25])
plt.xlabel('Diameter of Pizza')
plt.ylabel('Price of Pizza')
plt.title('R-squared(Degree=4): %.3f' % regressor_poly4.score(x_train_poly4, y_train))
plt.legend(handles=plt1+plt2+plt4)
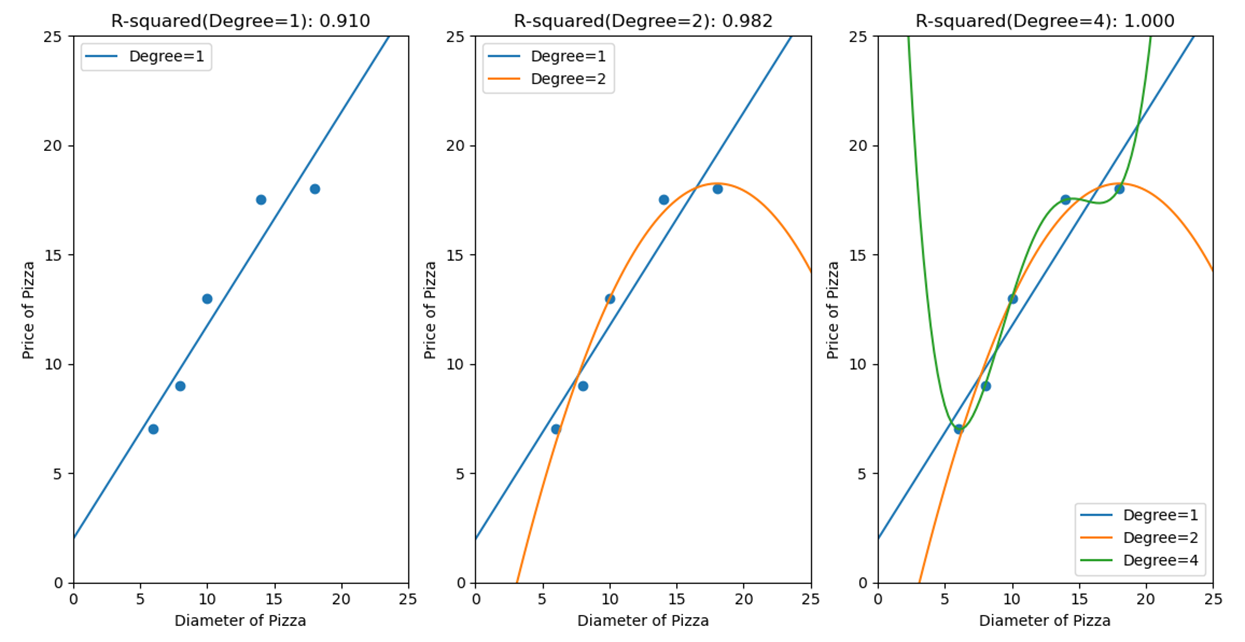
plt.show()三种模型分别是线性回归、2次多项式回归和4次多项式回归,下面直接上图
图标题是R-squared评价值,前文有提到,很明显,1、4分别是欠拟合和过拟合,为了平衡增加模型复杂度来提高性能表现和模型缺乏泛化力的矛盾,需要对模型正则化。
L1/L2范数正则化
二者都是在原模型优化目标的基础上,增加对参数的惩罚项。L1范数正则化通过让参数向量中许多元素趋向于0,使得大部分特征失去对优化目标的贡献,有效特征变得稀疏;L2范数正则化会让参数向量中的大部分元素都变得很小,压制参数之间的差异性。本小节使用上节4次多项式拟合模型来做实验,代码如下:
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# 输入样本特征以及目标值,即披萨直径
x_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
# 准备测试数据
x_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]
poly4 = PolynomialFeatures(degree=4)
# 映射出4次多项式特征
x_train_poly4 = poly4.fit_transform(x_train)
regressor_poly4 = LinearRegression()
regressor_poly4.fit(x_train_poly4, y_train)
# 使用测试数据对4次多项式回归模型的性能进行评估
x_test_poly4 = poly4.transform(x_test)
print(regressor_poly4.score(x_test_poly4, y_test), '\n',
'普通4次多项式回归模型的参数列表:', regressor_poly4.coef_)
'''L1范数正则化,Lasso模型在4次多项式特征上的拟合表现'''
from sklearn.linear_model import Lasso
# 使用Lasso对4次多项式进行拟合
lasso_poly4 = Lasso()
lasso_poly4.fit(x_train_poly4, y_train)
print(lasso_poly4.score(x_test_poly4, y_test), '\n',
'Lasso模型的参数列表:', lasso_poly4.coef_)
'''L2范数正则化,Ridge模型在4次多项式特征上的拟合表现'''
from sklearn.linear_model import Ridge
# 使用Lasso对4次多项式进行拟合
ridge_poly4 = Ridge()
ridge_poly4.fit(x_train_poly4, y_train)
print(ridge_poly4.score(x_test_poly4, y_test), '\n',
'Ridge模型的参数列表:', ridge_poly4.coef_, '\n',
'Ridge模型拟合后参数的平方和:', np.sum(ridge_poly4.coef_**2))| 运行结果如下: 0.8095880795766807 普通4次多项式回归模型的参数列表: [[ 0.00000000e+00 -2.51739583e+01 3.68906250e+00 -2.12760417e-01 4.29687500e-03]] 0.8388926873604382 Lasso模型的参数列表: [ 0.00000000e+00 0.00000000e+00 1.17900534e-01 5.42646770e-05 -2.23027128e-04] 0.8374201759366577 Ridge模型的参数列表: [[ 0. -0.00492536 0.12439632 -0.00046471 -0.00021205]] Ridge模型拟合后参数的平方和: 0.015498965203571016 |
可以看到,两种范数模型都对没有正则化的模型有一定的优化作用,均提高了三个百分点,此外观察两个模型的参数列表也呼应了其对应的惩罚机理。
模型检验
模型检验即对训练好的模型进行测试,根据验证流程复杂度不同,分为留一验证和交叉验证。留一验证就是前面一直使用的方法,将完整数据集划分为训练集和测试集,比例通常为7:3。交叉验证可以理解为进行多次留一验证的过程,每次用作验证的验证集是互斥的,并且保证每条数据都经验证。比如3折交叉验证就是每次迭代选取其中一组数据作为验证集,另两组作为训练集。
超参数搜索
前面提到的模型配置,这些不同的配置称作模型的超参数,多数情况下,超参数是无限的,只能在一定的差参数组合空间内进行暴力搜索,以比较获取最优性能模型。
网格搜索&并行搜索
网格搜索即在某个超参数组合空间中,使用交叉验证的方法同样的训练集和测试集下进行训练和评估模型,但这样通常会耗费很多时间,并行搜索是利用多核处理器甚至是分布式资源来计算,因为各个新模型在执行交叉验证的过程中是相互独立的,这样来成倍节省运算时间。本节在并行网格搜索的背景下,使用朴素贝叶斯模型对前文提到的20类新闻数据前30000条进行分类,代码如下:
import numpy as np
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.svm import SVC
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.pipeline import Pipeline
news = fetch_20newsgroups(subset='all')
# 对前3000条新闻文本进行数据分割
x_train, x_test, y_train, y_test = train_test_split(
news.data[:3000], news.target[:3000], test_size=0.25, random_state=23)
# 使用Pipeline简化系统搭建流程,将文本抽取与分类器模型串联起来
clf = Pipeline([('vect', TfidfVectorizer(stop_words='english', analyzer='word')),
('svc', SVC())])
# 需要实验的两个超参数的个数分别是4、3,共有12种参数组合模型
parameters = {'svc__gamma': np.logspace(-2, 1, 4),
'svc__C': np.logspace(-1, 1, 3)}
# 初始化并行网格搜索,n_job=-1代表使用该计算机的全部CPU
gs = GridSearchCV(clf, parameters, verbose=2, refit=True, cv=3, n_jobs=-1)
gs.fit(x_train, y_train)
print(gs.best_params_, gs.best_score_)
# 输出最佳模型在测试集上的准确性
print(gs.score(x_test, y_test))| 截取部分运行结果: [Parallel(n_jobs=-1)]: Done 36 out of 36 | elapsed: 1.5min finished |
最佳模型在测试集上的准确性: 0.8293333333333334
超参数共有12种组合,代码中已做了注释,再进行3折交叉验证,即36项独立的计算机任务,这里我电脑的运行时间是一分半钟,我电脑是双核的,单线程也就是需要3分钟,符合书中结果。再有这个准确性是不能与前面的新闻分类实例做比较的,因为数据集和数据分割策略都不相同。
就写到这里吧,后面是一些流行库/模型的介绍和示例以及几个kaggle竞赛的经典题目,对应的官网上也应该会有很多有意思的示例。
或扫码搜索关注微信公众号“燕山徐一”,后台回复“python机器学习”获取代码。